Проектирование манипулятора

Куклин А.А. Чертеж зоны обслуживания.cdw

Курсовая работа по ТММ.docx

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОСИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВПО «ИЖЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. М.Т. КАЛАШНИКОВА»
КАФЕДРА «МЕХАТРОННЫЕ СИСТЕМЫ»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОМУ ПРОЕКТУ
по дисциплине «Теория машин и механизмов»
на тему «Проектирование манипулятора»
Рецензент: Чухланцев Е.С.
ПРЯМАЯ ЗАДАЧА О ПОЛОЖЕНИЯХ5
ПРЯМАЯ ЗАДАЧА КИНЕМАТИКИ О ПОЛОЖЕНИЯХ7
ТЕНЗОРНО-МАТРИЧНЫЙ МЕТОД7
МЕТОД РАСШИРЕННЫХ МАТРИЦ ПЕРЕХОДА12
РАСЧЕТ И ПОСТРОЕНИЕ ЗОНЫ ОБСЛУЖИВАНИЯ17
ПРЯМАЯ ЗАДАЧА О СКОРОСТЯХ И УСКОРЕНИЯХ20
ТЕНЗОРНО-МАТРИЧНЫЙ МЕТОД20
ПРОЧНОСТНОЙ РАСЧЕТ45
В середине прошлого века в машино- и приборостроении появилось новое поколение станков автоматов управляемых с помощью специально разработанных программ.
Применение станков с ЧПУ (числовым программным управлением) позволило автоматизировать производство машиностроительных отраслей. Поиск новых концепций в процессах автоматизации привел к разработке нового вида станков которым было дано название – промышленные роботы манипуляторы.
Основное назначение робота манипулятора состоит в замене человека:
- при выполнении монотонных видов работ
- в зоне действия агрессивных сред
- при перемещении тяжелых грузов.
Робот манипулятор каждое свое действие выполняет согласно заданного программой алгоритма рассчитанного для данной технологической операции. Такой принцип работы свойственен для однообразных повторяющихся операций.
Программа позволяет обеспечить высокую точность выполнения команд за счет расчета траектории для движения руки робота манипулятора.
Робот-манипулятор выполняющий команды оператора передаваемые с помощью пульта дистанционного управления используется в условиях опасных для жизни человека. При этом контроль выполнения роботом команд ведется визуально и с применением промышленного телевидения. Когда передающая видеосигнал камера встраивается в манипуляторе таким образом чтобы обеспечить максимальный обзор.
В зависимости от сложности выполняемых операций определяется количество степеней свободы которыми должна обладать робот рука-манипулятор в связи с этим в них применяют два типа подвижных звеньев:
- для возвратно-поступательных движений
- для угловых и радиальных перемещений.
Чем сложнее заданная траектория движения тем больше степеней свободы должна иметь робот рука-манипулятор. Ее движение может осуществляться с помощью приводов с использованием:
Захватные устройства в виде щупов (механических пальцев) по своим действиям аналогичные руке человека наиболее универсальны и получили название робот рука-манипулятор.
Для определенных видов работ вместо щупов используют краскопульт или автоматическую отвертку клещи для сварки или специально сконструированную головку для захвата деталей сложной конфигурации.
Одним из главных положительных моментов при применении робототехники в производствах требующих высокой точности выполнения монотонных операций является отсутствие влияния человеческого фактора.
Промышленные роботы манипуляторы выполняя работу в опасных для жизни человека условиях сохраняют здоровье обслуживающего персонала.
При возможности круглосуточного использования в производстве при доле брака на уровне 1-3% быстро окупаются.
Манипуляторы широко применяются:
– в автомобилестроении;
– в деревообрабатывающей промышленности;
– на химическом производстве и др.
ПРЯМАЯ ЗАДАЧА О ПОЛОЖЕНИЯХ
Выполним структурный анализ кинематической схемы манипулятора представленной на рис. 1.
Рисунок 1 – Кинематическая схема трехзвенного манипулятора.
У представленного механизма 3 подвижных звена: 1 2 и 3.
Начало системы координат и звено 1 образуют вращательную кинематическую пару А. Пара одноподвижная число степеней свободы звена Н=1. Класс кинематической пары S = 6-Н = 6-1 = 5.
Звенья 1 и 2 образуют поступательную пару В. Пара одноподвижная число степеней свободы Н=1.
Звенья 2 и 3 образуют вращательную пару С. Пара одноподвижная число степеней свободы Н=1.
Рабочим органом (схватом) манипулятора является точка D.
Степень подвижности механизма определяется по формуле Чебышева для пространственных механизмов:
W = 6n-5p5 = 6*3-5*3 = 3 (1)
где n – число звеньев p5 – количество кинематических пар пятого класса.
Таким образом для придания определенности движению манипулятора следует задать движение всем трем его звеньям.
ПРЯМАЯ ЗАДАЧА КИНЕМАТИКИ О ПОЛОЖЕНИЯХ
Прямая задача о положениях состоит в определении абсолютных положений звеньев при их заданных относительных положениях.
ТЕНЗОРНО-МАТРИЧНЫЙ МЕТОД
Для определения величины результирующего радиуса-вектора крайней точки многозвенного механизма необходимо составить соответствующее матричное уравнение характеризующее положение крайней точки относительно базовой системы координат.
Для тензорно-матричного метода нет необходимости изменения систем координат звеньев. Достаточно записать соответствующие матрицы поворота и переноса для базовой системы координат совмещенной с системами координат соответствующих звеньев. При решении прямой задачи о положении схвата манипулятора обычно используют метод преобразования координат.
Рассмотрим трехмерную декартовую систему координат являющуюся правосторонней. Примем соглашение в соответствии с которым будем считать положительными такие повороты при которых (если смотреть с конца полуоси в направлении начала координат) поворот на 90° против часовой стрелки будет переводить одну полуось в другую. На основе этого соглашения строится следующая таблица которую можно использовать как для правых так и для левых систем координат:
Положительным будет направление поворота
Матрицы поворота М определяют поворот системы координат соответствующего звена для корреляции относительно предыдущего по порядку. В зависимости от поворота вокруг соответствующей оси выделяется три стандартных типа матриц поворота. Повороты вокруг осей Х Y и Z определяются соответственно матрицами:
Подставляя значения углов поворота относительно соответствующих осей определяем матрицы поворота.
В сочетании с матрицами поворота учитываются так называемые матрицы переноса L по факту являющиеся векторами. Они определяют линейные смещения систем координат звеньев друг относительно друга. В общем виде матрица L имеет следующий вид:
Положение схвата манипулятора описываемое радиус вектором
определяется векторным уравнением сочетающим комбинацию длин векторов переноса с перемещениями звеньев и матриц переноса . Построение уравнения начинается с крайнего звена и по порядку вплоть до начального.
Каждое следующее добавление нового элемента в выражение по определению положения схвата сопровождается либо добавлением нового слагаемого в виде линейного перемещения звена либо матрицы поворота при угловом перемещении [2 5].
Рассмотрим пример расчета положения схвата для кинематической схемы манипулятора представленной на рис. 1 тензорно-матричным методом с учетом представленных в таблице 1 исходных данных для расчета.
Выражение для радиус-вектора точки выходного звена в соответствии с правилами построения принимает следующий вид:
На рисунке 2 проиллюстрировано построение систем координат звеньев в соответствии с тензорно-матричным методом. Для всех кинематических пар ориентация звеньев остается постоянной с тем отличием что происходит корректирование угла поворота в случае вращательного движения (и ) и дополнительный перенос в случае поступательного движения . При условии что система координат совпадает с а – с .
Рисунок 2 – Системы координат и параметры трехзвенного манипулятора для тензорно-матричного метода расчета задачи о положениях.
Звено 1 вращается относительно стойки и базовой системы координат вокруг оси Z. Соответственно в уравнении (8) учитывается длина звена 1 вдоль оси Z:
и матрица поворота вокруг оси Z:
является общей для всех последующих звеньев механизма после первого. Второе звено – поступательное поэтому вместо матрицы поворота учитывающей обобщенные угловые координат используется матрица переноса с обобщенной линейной координатой выраженной перемещением второго звена относительно первого вдоль оси X в отрицательном направлении:
Длина звена 2 учитывается вектором:
Третье звено является последним в кинематической схеме и определяется матрицей поворота вокруг оси X:
и длиной двусоставного звена
Знак «–» указывает на отрицательно направление звеньев относительно осей.
Подставляя значения матриц (8-13) в (7) определим значение радиус-вектора схвата в общем виде:
Подставим в выражение (15) общие численные значения для обобщенных переменных и геометрических параметров кинематической схемы из таблицы 1 определив в координатах положение схвата манипулятора для общего расчета:
МЕТОД РАСШИРЕННЫХ МАТРИЦ ПЕРЕХОДА
При решении прямой задачи о положении схвата манипулятора обычно используют метод преобразования координат. Из множества методов преобразования координат которые отличаются друг от друга правилами выбора осей локальных систем координат для манипуляторов обычно используется метод Денавита и Хартенберга. При использовании данного метода оси координат располагаются по следующим правилам.
Для звена i ось zi направляется по оси кинематической пары образуемой им со звеном (i+1). Начало координат размещают в геометрическом центре этой пары.
Ось xi направляется по общему перпендикуляру к осям zi-1 и zi с направлением от zi-1 к zi. Если оси zi-1 и zi совпадают то xi перпендикулярна к ним и направлена произвольно. Если они пересекаются в центре кинематической пары то начало координат располагается в точке пересечения а ось xi направляется по правилу векторного произведения (кратчайший поворот оси zi до совмещения с zi-1 при наблюдении с конца xi должен происходить против часовой стрелки).
Ось yi направляется так чтобы система координат была правой.
В прямой задаче необходимо определить положение схвата манипулятора и связанной с ним системы координат по отношению к неподвижной или базовой системе координат. Это осуществляется последовательными переходами из системы координат звена i в систему координат звена i-1. Согласно принятому методу каждый переход включает в себя последовательность четырех движений: двух поворотов и двух параллельных переносов осуществляемых в указанной последовательности:
поворот вокруг оси zi-1 на угол до тех пор пока ось
перенос вдоль оси zi-1 на величину после которого начало системы координат Oi оказывается в начале координат Oi-1 системы (i-1) (отсчитывается по оси zi-1 от ее начала координат Oi-1 до точки ее пересечения с осью
поворот i-ой системы вокруг оси xi на угол до параллельности осей zi и zi-1 (положительное направление поворота при наблюдении с конца вектора xi против часовой стрелки).
Необходимо отметить что знак угла поворота не имеет значения так как в матрицах перехода используются направляющие косинусы (четные функции). Целесообразно рассматривать угол обеспечивающий кратчайший поворот оси старой системы i до совмещения (параллельности) с соответствующей осью новой (i-1). Перемещения начала координат определяются как координаты начала старой системы Oi в новой Oi-1.
В манипуляторах обычно используются одноподвижные кинематические пары или вращательные или поступательные. Оба относительных движения как вращательное так и поступательное реализуются в цилиндрических парах. Поэтому при общем представлении механизма используются цилиндрические пары. Опуская описание матриц поворота и переноса относительно осей x и z запишем матрицу перехода из i-ой системы координат в (i - 1)-ю:
В матрицу входят четыре параметра: . Для любой кинематической пары три из них являются константами и только один – переменной величиной. Для вращательной пары (В) переменная величина – угол для поступательной пары (П) – перемещение . Тогда матрица содержит только одну переменную величину называемую обобщенной координатой. (МПР)
Прямая задача кинематики о положениях решается с помощью следующей формулы:
где матрица равная произведению матриц :
В формуле (18) и - матрицы-столбцы размером первые три элемента которых – это координаты произвольной точки схвата соответственно в системах n и 0. [2]
Рассмотрим пример расчета положения схвата для кинематической схемы манипулятора представленной на рис. 1 методом расширенных матриц перехода с учетом представленных в таблице 1 исходных данных для расчета.
На первом этапе необходимо на основе кинематической схемы данной в задании (рис. 1) составить новую кинематическую схему учитывающую изменение ориентации систем координат звеньев (рис. 3). На схеме указываются системы координат звеньев начиная с базовой и обобщенные координаты.
Рисунок 3 – Системы координат и параметры трехзвенного манипулятора.
На втором этапе составляется таблица кинематических пар и параметров вида табл.2. Углы и соответствуют общим значениям углов поворота (табл. 1) при повороте относительно осей вращения и соответственно. Угол в соответствии с рис. 3. составляет 90 градусов если смотреть на поворот оси до совмещения с осью с конца оси . Перенос соответствует длине первого звена (табл. 1). Для системы координат второго звена характерен параметр соответствующий суммарной величине длины второго звена и продольного перемещения (табл. 1). Для составного третьего звена принимаем значения и (табл. 1).
На третьем этапе в соответствии с (17) составляются расширенные матрицы перехода для каждого из сочленений с учетом значений приведенных в табл. 2:
Далее из произведения расширенных матриц перехода звеньев запишем вектор столбец значений
Подставляя значения параметров и длин звеньев в (23) получим координаты (первые три значения) положения схвата манипулятора для общего положения с учетом системы координат принятой в соответствии с рис. 3:
РАСЧЕТ И ПОСТРОЕНИЕ ЗОНЫ ОБСЛУЖИВАНИЯ
Построение зоны обслуживания манипулятора требует проведения расчета значений радиус-вектора схвата для минимально достаточного количества крайних положений с экстремальными значениями обобщенных координат. Это количество можно определить зависимостью то есть для трехзвенного манипулятора количеством таких точек будет 8 а например для четырехзвенного – 16. Расчет может производиться в одном из доступных математических пакетов табличного редактора пакета Office либо путем написания собственной программы расчета на одном из доступных языков программирования. По полученным данным формируется таблица значений (табл. 3) и осуществляется построение графической модели зоны обслуживания манипулятора (лист формата А3) в одном из доступных графических пакетов либо путем написания собственного графопостроителя на одном из доступных языков программирования.
Анализируя данные таблицы можно сделать следующие выводы. При повороте первого звена на углы в 180 градусов и 360 (0) градусов значения принимает только составляющая X координат схвата на углах 90 градусов и 270 градусов соответственно составляющая Y. Обе координаты – горизонтальные соответственно определяются длиной второго звена с учетом продольного перемещения а так же горизонтальной составляющей третьего звена. При углах поворота первого звена отличных от названных горизонтальный габарит зоны обслуживания схвата распределяется между осями X и Y. Разброс максимальных значений обусловлен обобщенным параметром второго звена . Составляющая по оси Z – вертикальная и определяется длиной первого звена и вертикальной составляющей третьего звена. Третье звено вращательное поэтому имеем разброс значений Z в один метр учитывая длину и вращение третьего звена на 360 градусов.
Пример зоны обслуживания для кинематической схемы представленной на рис. 1 изображен на рис. 3.
Построение может осуществляться и упрощенным образом без формирования таблицы а с использованием аналитических навыков. Выбирается одна из секущих областей в нашем случае например Х0Z для кинематической схемы представленной на рис. 1. Если относительно базовой системы координат первым звеном осуществляется вращательное движение то производится условная операция «вращения» для построения полной зоны обслуживания в зависимости от угла поворота (в нашем случае поворот вокруг оси Z на 360 градусов). Если вид движения первого звена – поступательное то производится операция «вытягивание» в зависимости от продольного перемещения . В рассматриваемом примере вид секущей плоскости – прямоугольник образованный в результате наложения двух движений: второго звена поступательное – горизонтальная составляющая вдоль оси Х; третьего звена вращательное – вертикальная составляющая (по оси Z) получаемая вращением вокруг оси Х.
Рисунок 4 – Зона обслуживания трехзвенного манипулятора.
ПРЯМАЯ ЗАДАЧА О СКОРОСТЯХ И УСКОРЕНИЯХ
Прямая задача о скоростях и ускорениях состоит в определении абсолютных величин линейных скоростей и ускорений точек звеньев манипулятора и абсолютных угловых скоростей и ускорений звеньев при заданных относительных величинах.
Решение выполняется на базе основных зависимостей теории механизмов и машин для скоростей и ускорений. Однако все выражения записываются в векторном виде учитывающем составляющие параметров по осям координат. Основным отличием решения задачи о скоростях и ускорениях для пространственной конструкции манипулятора от плоских механизмов является необходимость нахождения проекций единичных векторов соответствующих осей шарниров при определении угловых параметров и проекций звеньев при определении линейных параметров на оси базовой системы координат .
В состав кинематической цепи манипулятора (рис.4.) входят три подвижных звена вращательные А и С и поступательная В кинематические пары V класса. Их положение в пространстве а также положение точки D схвата характеризуется длинами звеньев линейными и угловыми обобщенными координатами (расчетные значения) известны линейные и угловые относительные скорости и ускорения звеньев руки (табл. 4).
Определить угловые скорости всех звеньев руки манипулятора а также линейные скорости и ускорения точек B C и D.
Проекции единичных векторов и соответствующих осей шарниров А и С на оси системы координат описываются матрицами:
Для звена 1 определяем векторы угловой скорости и углового ускорения и соответствующие матрицы:
Рисунок 5 – Относительные кинематические параметры трехзвенного манипулятора
Для звена 2 угловую скорость и ускорение определяем с помощью векторных уравнений:
а так как и то получим и .
Векторы относительной угловой скорости и относительного углового ускорения характеризующие закон вращения звена 3 относительно звена 2 определяют по формулам:
а соответствующие им матрицы записываются в виде:
Для определения угловой скорости и углового ускорения третьего звена составляем векторные уравнения:
В эти уравнения входит векторное произведение которое как и произведение любых двух векторов описываемых матрицами:
в общем виде превращается в вектор с матрицей
Подставляя (27) и (28) в (31) получим матрицу-столбец вектора :
Подставив (25) (26) и (32) в (29) определяем матрицы
а по ним – модули векторов угловой скорости и углового ускорения:
Для определения проекций векторов и на оси координат записывают матричные уравнения
столбец координат точки D в системе м;
матрицы переноса соответственно от систем координат 1 к 0 и 2 к 1;
матрицы поворота при переходе соответственно от систем координат 1 к 0 и 3 к 2.
Подставив (35)-(37) в (34) получим матрицы
Запишем модули соответствующих векторов
Так как угол между векторами равен нулю то
Для определения скорости точки С используем векторное уравнение
Здесь откуда получаем матрицу
Пользуясь зависимостями (27) (31) и (39) определяем элементы матрицы-вектора :
Подставляя (41) и (42) в (40) получим матрицу-столбец вектора :
а также его величину
Пользуясь зависимостями (31) (33) и (38) определяем матрицу-столбец вектора :
а затем матрицу вектора как сумму матриц (43) и (45):
Вектор и угол между векторами равны нулю следовательно .
Используя зависимости (27) (31) и (38) составляем матрицу векторного произведения :
Для определения матрицы векторного произведения используем зависимости (27) (31) и (38):
Матрицу вектора ускорения Кориолиса составляют с использованием зависимостей (27) (31) и (41):
Складывая матрицы (49)-(52) получим матрицу вектора :
Модуль вектора ускорения
где матрицы входящих в уравнение векторных произведений определяют с использованием зависимостей (31) (33) (38) и (53):
Складывая матрицы (53) и (55) получим матрицу-столбец вектора :
откуда модуль вектора ускорения
Ось вращения первого звена относительно базовой системы координат совпадает с осью . Исходя из величины скорости равной по величине примем масштаб . Из полюса являющегося началом системы координат плана угловых скоростей проводим отрезок длиной 50 мм вдоль оси вращения Z (рис. 6). Скорость совпадает с так как второе звено совершает поступательное движение. Результирующая скорость имеет две составляющие: и . Скорость известна и в соответствии с рис. 5 направлена под углом 30 градусов к оси X в плоскости X. Из конца вектора проводим отрезок длиной 50 мм в указанном направлении. Соединяя точку полюса с концом построенного вектора получим искомый вектор . Измеряя длины отрезков можно получить значения искомых параметров и сравнить с аналитическим расчетом.
Рисунок 6 – План угловых скоростей.
Построение плана угловых ускорений (рис. 7) начинаем с определения полюса и величины масштаба в соответствии с угловым ускорением направленного как и вдоль оси Z. Примем масштаб . Из полюса являющегося началом системы координат плана угловых скоростей проводим отрезок длиной 50 мм. Ускорение второго звена совпадает с . По законам ТММ угловое ускорение третьего звена определяется следующим выражением:
Относительное ускорение равно и в соответствии с рис. 5 направлено под углом 30 градусов к оси Y в плоскости X. В указанном направлении из конца вектора в той же плоскости проводим отрезок длинной 50 мм характеризующий угловое ускорение третьего звена относительно первого. Составляющая имеет величину:
и направлена под углом 30 градусов к оси Y однако лежит в отрицательной области оси Х плоскости X. Из конца вектора проводим отрезок длиной 5 мм. Отрезок соединяющий полюс плана и конец вектора будет искомым угловым ускорением третьего звена.
Рисунок 7 – План угловых ускорений.
Построение плана линейных (рис. 8) скоростей начинаем с определения полюса . Точки О и А не имеют линейных скоростей. Точка В принадлежит поступательному звену однако лежит на линии вращения поступательного звена и потому равна нулю. Линейная скорость точки С складывается из двух составляющих: относительной скорости движения второго звена относительно первого и произведения угловой скорости второго звена на проекцию этого звена в абсолютной системе координат.
В соответствии с рис. 4 вектор скорости направляется противоположно оси X под углом в 30 градусов. Величина составляет 02 мс (табл. 4). Принимаем масштаб плана скоростей и проводим отрезок характеризующий длиной 20 мм. Составляющая угловой скорости в направлена перпендикулярно и равна произведению:
Из конца проводим отрезок длиной 175 мм и по правилу треугольника достраиваем вектор .
Построение скорости точки D осуществляется путем сложения скорости точки C и . Относительная скорость так как вид кинематической пары D – вращательная. На рис.8 скорость лежит в плоскости X так как движение второго звена осуществляется только относительно оси Z. Однако имеет уже три составляющие и лежит в пространстве образуя параллелепипед. Диагональ параллелепипеда лежит под углом 30 градусов к оси X и под углом 60 градусов к оси Z (в соответствии с рис. 5). Составляющая по оси Z определяется длиной а составляющие по осям Х и Y обоими элементами составного звена. Соединение точки полюса плана с концом построенного вектора дает искомый вектор .
Анализируя план линейных скоростей можно сказать что линейная скорость точки D в первую очередь определяется величиной скорости поступательного звена а вращательные звенья манипулятора в таком случае выступают в качестве ориентирующих.
Рисунок 8 – План линейных скоростей.
Построение плана линейных ускорений (рис. 8) начинаем с определения полюса . Точки О А и В не имеют линейных ускорений. Линейное ускорение точки С складывается из составляющих релятивного ускорения (обусловлено относительным ускорением второго звена относительно первого определяется аналогично переносной скорости направлено вдоль звена) нормального (обусловлено угловой скоростью второго звена определяется проецированием на базовую систему координат направлено к центру вращения с учетом проекции звена) касательного (обусловлено угловым ускорением второго звена определяется проецированием на базовую систему координат направлено перпендикулярно касательному ускорению) и ускорения Кориолиса (обусловлено сложным характером движения – вращательное второго звена и поступательное первого звена с учетом не параллельности главных осей звеньев):
С учетом правил построения векторов ускорений имеем что сонаправлены пары ускорений с и с . Как и для скорости результирующий вектор должен лежать в плоскости X. На первом этапе построения плана линейных ускорений выполним построение векторов составляющих . Вектор направлен противоположно (см. рис.5) – под углом 30 градусов к оси X. Из табл. 4 величина . Принимаем масштаб плана ускорений . Проводим отрезок длиной 40 мм. Аналогично направленный по второму звену вектор определяется произведением квадрата угловой скорости на длину второго звена:
Проводим отрезок длиной 35 мм из конца вектора в том же направлении. Перпендикулярно направленный вектору вектор определяется величиной:
Проводим отрезок длиной 35 мм из конца вектора в перпендикулярном направлении. Величина кариолисова ускорения определяется величиной:
Из конца вектора проводим отрезок длиной 8 мм характеризующий . Складывая длины четырех указанных векторов получаем ускорение .
Точка D принадлежит вращательному звену 3 потому ускорение не имеет составляющей релятивного ускорения а так как главные оси второго и третьего звеньев параллельны то отсутствует и кориолисово ускорение. Остаются составляющая а так же нормальная и тангенциальная составляющие:
Достраивая взаимно перпендикулярные вектора получаем искомое ускорение точки D – .
Анализируя план линейных ускорений делаем вывод о том что ускорение точки D в первую очередь определяется ускорением Кориолиса зависящим от достаточно высокого значения линейной скорости второго звена (см. табл. 4). Необходимо отметить и то что достаточно малы значения нормальной и касательной составляющих для третьего звена по причине малых габаритов этого звена. Пример плана линейных ускорений наглядно доказывает то что третье звено в манипуляторе предназначено в первую очередь для ориентирующей функции а кинематическую функцию исполняет второе звено.
Рисунок 9 – План линейных ускорений.
Расчет звеньев на прочность начинается с последнего звена манипулятора так как масса самих звеньев еще не определена. Звенья манипулятора необходимо расположить таким образом чтобы на него действовали максимальные изгибающие моменты.
Каждое отдельно взятое звено можно рассматривать как балку с криволинейной или прямолинейной осью закрепленную консольно. Следовательно в заделке может возникнуть от трех (плоский случай 2 силы и один момент) до шести (пространственный случай 3 силы и 3 момента) реакций.
Рисунок 10 – Схема нагружения третьего звена.
Под действием веса детали Qгр и распределенной нагрузки от веса звена q3 в балке с криволинейной осью возникают следующие внутренние силовые факторы:
Q – поперечная сила от веса груза и звена
- изгибающий момент относительно оси Y на участке l3
Так как вес звена неизвестен то на первом этапе учитываем только действие груза
Эквивалентная нагрузка в опасном сечении по третьей теории прочности определяется
Момент сопротивления поперечного сечения определяется
где n - коэффициент запаса прочности n=10 так как определяющим фактором в конечном итоге является жесткость руки манипулятора;
- допускаемые напряжения =160 МПа.
Исходя из условий работы (вращение вокруг оси Х на 3600) наиболее предпочтительным является сечение в виде кольца или квадрата.
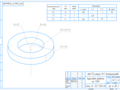
Рисунок 11– Сечение третьего звена манипулятора.
Для кольцевого сечения имеем
где D - диметр наружного цилиндра;
d - диаметр отверстия.
Принимаем =34 мм тогда =17 мм.
- удельный вес стали =000785 грмм3 (7854*10-6 кгмм3).
Распределенная нагрузка от веса звена
Пересчитываем вес звена с учётом распределённой нагрузки
Принимаем D=40 мм тогда d=20 мм.
Рисунок 12 – Схема нагружения второго звена.
Так как вес звена 2 неизвестен то учитываем только действие груза и уже рассчитанный вес звена 3
Исходя из условий работы (поступательное движение вдоль оси Х) наиболее предпочтительным является прямоугольное сечение.
Рисунок 13 – Сечение второго звена.
Для прямоугольного сечения имеем:
Используем следующую формулу для определения массы звена:
Распределенная нагрузка равна:
Пересчитываем вес звена с учётом распределённой нагрузки:
h=0.75H=0750052=0039 м
S=HB-hb=00520026-00390013=0000845 м2
m2 = V * γ = (S * L2)* γ = 1161 кг
Рисунок 14 – Cхема нагружения первого звена.
Поперечная сила от груза и звена:
Q12 = Qгр + (m+ m3 +m2)*g
Изгибающий момент Миу относительно оси Y:
Q12 = Qгр + (m+ m3+m2)*g =(50+1257+1161)*98=28596 Н
Миу = Qгр*X1 =28596*2=57192 Н м
Исходя из условий работы (вращение вокруг оси Z на 3600) наиболее предпочтительным является сечение в виде кольца или квадрата.
Рисунок 15 – Сечение первого звена манипулятора.
Принимаем =73мм тогда =365 мм.
Принимаем D=74 мм тогда d=37 мм.
Для стали [] = 160 мПа.
- эквивалентное напряжение звена
Найдем действующие моменты сопротивления:
Все полученные напряжения меньше допускаемого [] = 160 мПа.
На основе прочностного расчета делаем вывод о готовности выдержать критические нагрузки звеньев манипулятора с полученными формами и размерами.
Данная курсовая работа позволяет закрепить знания по курсу «Теория машин и механизмов» применительно к пространственным механизмам представляющим механическую часть манипулятора. В ходе выполнения курсовой работы был проведен структурный анализ заданной конструкции манипулятора. Были выполнены основные задания курсовой работы.
Произведен кинематический анализ механической части манипулятора. Составлены векторные уравнения для определения положения схвата манипулятора при известных длинах звеньев и их перемещениях. Определены основные параметры зоны обслуживания. Составлены векторные уравнения для определения угловых и линейных скоростей и ускорений звеньев кинематических пар и схвата манипулятора. Используя Определены скорости и ускорения для расчетного положения манипулятора. Для расчетного положения манипулятора построены планы скоростей и ускорений. Проведен силовой анализ заданной конструкции манипулятора.
Проведен прочностной расчет звеньев манипулятора. Определены геометрические характеристики поперечных сечений с учетом характера и вида нагружения. Найдены массы звеньев.
Также была рассчитана рабочая зона обслуживания манипулятора - пространство в котором может находиться рабочий орган манипулятора при его функционировании.
На основе полученных данных делаем вывод о готовности выдержать критические нагрузки звеньев манипулятора с полученными формами и размерами.
Данный расчет служит базой для выработки навыков проектирования и расчета подобных устройств но он является лишь ориентировочным расчетом так как не учитывались массы приводов и двигателей установленных на звеньях.
Артоболевский И.И. Теория механизмов и машин.- М.: Наука 1975.-639 с.
Попов С. А. Курсовое проектирование по теории механизмов и машин. - М.: Высшая школа 1986.-295 с.
Борисенко Л. А. Теория механизмов машин и манипуляторов. -М.: Инфра-М 2011.- 285 с.
Белянин П. Н. Промышленные роботы. -М.: Машиностроение 1975.-400 с.