Центральные проекции и их основные свойства
Для проецирования произвольной точки через нее и центр проекций проводят прямую. Точка пересечения этой прямой с плоскостью проекций и является центральной проекцией заданной точки на выбранной плоскости проекций.
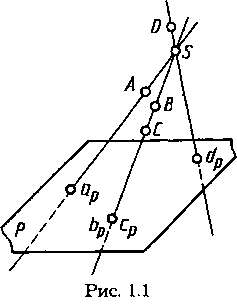
На рисунке 1.1 центральной проекцией точки А является точка ар пересечения прямой SA с плоскостью Р. Так же построены центральные проекции bр, ср, dpточек В, С, D на плоскости Р.
Прямые, проходящие через центр проекций и проецируемые точки, называют проецирующими прямыми. Центральные проекции bр и ср двух различных точек В и С в пространстве, которые располагаются на одной проецирующей прямой, совпадают. Все множество точек пространства, принадлежащих одной проецирующей прямой, имеет при одном центре проецирования одну центральную проекцию на заданной плоскости проекций.
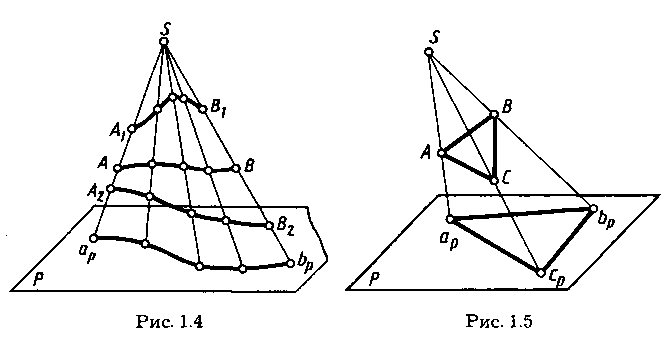
Следовательно, при заданных плоскости проекций и центре проецирования одна точка в пространстве имеет одну центральную проекцию. Но одна центральная проекция точки не позволяет однозначно определить положение точки в пространстве. Для обеспечения обратимости чертежа, т. е. однозначного определения положения точки в пространстве по ее проекции, нужны дополнительные условия, например, можно задать второй центр проекций. Центральным проецированием может быть построена проекция любой линии или поверхности как множество проекций всех ее точек (см. рис. 1.2, 1.3). При этом проецирующие прямые (в своей совокупности), проведенные через все точки кривой линии, образуют проецирующую коническую поверхность (рис. 1.2) или могут оказаться в одной плоскости (см. рис. 1.3), которая называется проецирующей. Проекция кривой линии представляет собой линию пересечения проецирующей конической поверхности с плоскостью проекций. Так, на рисунке 1.2 проецирующая коническая поверхность Q пересекается с плоскостью проекций Р по кривой apbp, являющейся проекцией линии АВ. Однако проекция линии не определяет проецируемую линию, так как на проецирующей поверхности может быть бесчисленное количество линий, проецирующихся в одну и ту же линию на плоскости проекций (рис. 1.4). При проецировании прямой линии, не проходящей через центр проекций, проецирующей поверхностью служит плоскость. Так, на рисунке 1.3 проецирующая плоскость Т, образуемая проецирующими прямыми SC и SD, проходящими через точки С и D прямой, пересекает плоскость проекций Р по прямой cpdp, которая и является проекцией прямой CD. Соответственно проекция тр Для построения проекций линий, поверхностей или тел часто достаточно построить проекции лишь некоторых характерных точек. Например, при построении на плоскости проекций Р проекции треугольника ABC (рис. 1.5) достаточно построить проекции ар, bр, ср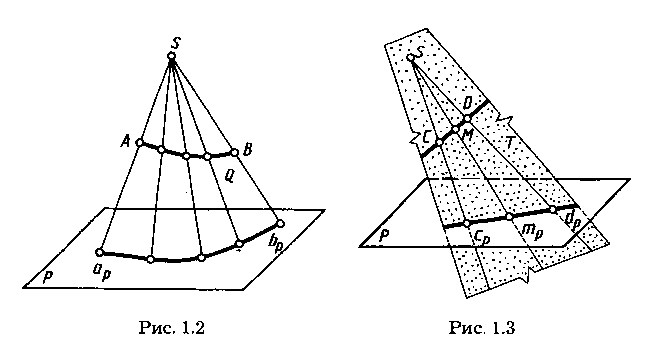
Свойства центрального проецирования.
1. При центральном проецировании:
а) точка проецируется в точку;
б) прямая, не проходящая через центр проекций, проецируется в прямую (проецирующая прямая — в точку);
в) плоская (двумерная) фигура, не принадлежащая проецирующей плоскости, проецируется в виде двумерной фигуры (фигуры, принадлежащие проецирующей плоскости, проецируются вместе с ней в виде прямой);
г) трехмерная фигура отображается двумерной.
2. Центральные проекции фигур сохраняют взаимную принадлежность, непрерывность и некоторые другие геометрические свойства.
3. При заданном центре проецирования проекции фигуры на параллельных плоскостях подобны.
4. Центральное проецирование устанавливает однозначное соответствие между фигурой и ее изображением, например изображения на киноэкране, фотопленке.
Центральные проекции применяют для изображения предметов в перспективе. Изображения в центральных проекциях наглядны, но для технического черчения неудобны, так как не соблюдается метрика.
