Прямоугольное (ортогональное) проецирование
Частный случай параллельного проецирования, при котором направление проецирования перпендикулярно плоскости проекций, называют прямоугольным или ортогональным проецированием. Прямоугольной (ортогональной) проекцией точки называют основание перпендикуляра, проведенного из точки на плоскость проекций. Прямоугольная проекция dp точки D показана на рисунке 1.9.
Наряду со свойствами параллельных (косоугольных) проекций ортогональное проецирование имеет следующее свойство:
ортогональные проекции двух взаимно перпендикулярных прямых, одна из которых параллельна плоскости проекций, а другая не перпендикулярна ей, взаимно перпендикулярны.
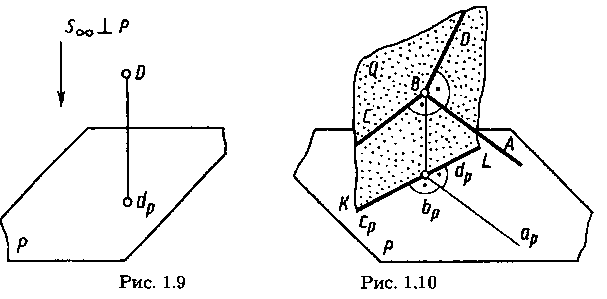
Докажем это. На рисунке 1.10 угол АВС= 90°; (АВ) || Р; (СВ) не перпендикулярно Р. Докажем, что угол арbрср= 90°.
Проецирующая прямая Вь, перпендикулярна плоскости проекций Р и прямой ВА. Прямая ВА перпендикулярна плоскости Q (Q включает Bbp; Q включает BC), так как прямая ВА перпендикулярна двум пересекающимся прямым этой плоскости (а угол ABbp = 90° — по условию, а угол АВbР= 90° — по построению). Проекция bpap перпендикулярна плоскости Q, так как (bpap) || (ВА). Следовательно, проекция плоскости Q на плоскости Р — прямая KL, перпендикулярная проекции bpap. Но с прямой KL совпадает проекция ьрср, т. е. угол арbрср= 90°, что и требовалось доказать.
Соответственно при угле DBA = 90°, (DB) не перпендикулярно Р и (АВ) || Р имеем:
угол dpbpap= 90°.
Ортогональное проецирование имеет ряд преимуществ перед центральным и косоугольным параллельным проецированием. К ним, в первую очередь, относятся простота геометрических построений ортогональных проекций точек и сохранение на проекциях при определенных условиях формы и размеров проецируемой фигуры.
Указанные преимущества обеспечили применение ортогонального проецирования для разработки чертежей во всех отраслях промышленности и в строительстве.
