Проецирование отрезка и деление его в данном отношении
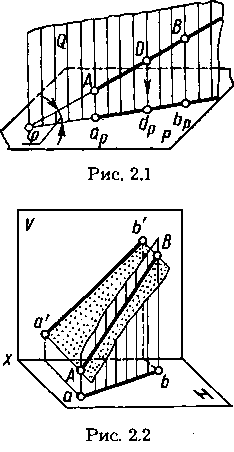
Наглядное изображение отрезка АВ прямой и его ортогонального проецирования на плоскость Р показано на рисунке 2.1. Рассмотрим ортогональное проецирование отрезка АВ с учетом свойств параллельного проецирования (1.2). Параллельные проецирующие прямые Аар и ВbР, проведенные из точек А и В прямой, образуют проецирующую плоскость Q, пересекающуюся с плоскостью проекций Р. Линия пересечения плоскостей Р и Qпроходит через проекции ари bр точек А и В на плоскости проекций Р. Эта линия и является единственной проекцией прямой на плоскости проекций Р.
Между длинами отрезка АВ прямой и его проекции арbр имеется зависимость |apbр| = |АВ| cosφ, где φ — угол между отрез
ком и плоскостью проекций. При φ=0 отрезок проецируется в натуральную величину; при φ=90° отрезок проецируется в точку. В остальных случаях длина проекции отрезка меньше длины самого отрезка.
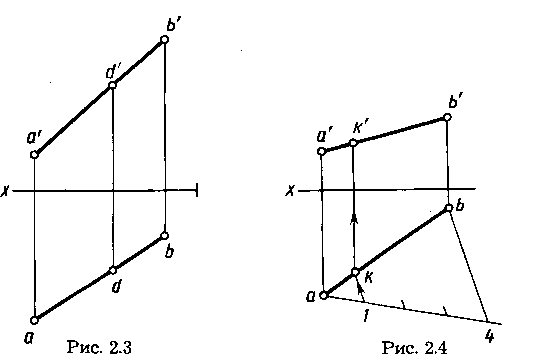
Наглядное изображение проецирования отрезка АВ прямой на две плоскости проекций в системе V, Н показано на рисунке 2.2, чертеж — на рисунке 2.3.
Если какая-либо точка принадлежит прямой, то ее проекция принадлежит проекции прямой. Например, точка D (см. рис. 2.1) принадлежит прямой АВ, ее проекция dp — проекция арbр. На рисунке 2.3 точка с проекциями d' и d принадлежит прямой с проекциями a'b', ab.
Если точка на отрезке делит его длину в данном отношении, то проекция точки делит длину одноименной проекции отрезка в том же отношении (см. рис. 1.8). Например, на рисунке 2.1 отношение | АВ| / | DB | = | apdp| / | dpbp|. Для рисунка 2.3 — отношения | a'd' | / | d'b'| и |ad| / | ab | равны отношению | AD | / | DB |.
Пример построения на чертеже проекций к' и к точки К, делящей отрезок с проекциями a'b', ab в отношении 1:3, показан на рисунке 2.4.
