Проецирование на две взаимно перпендикулярные плоскости проекций

Обратимость чертежа может быть обеспечена проецированием на две непараллельные плоскости проекций.

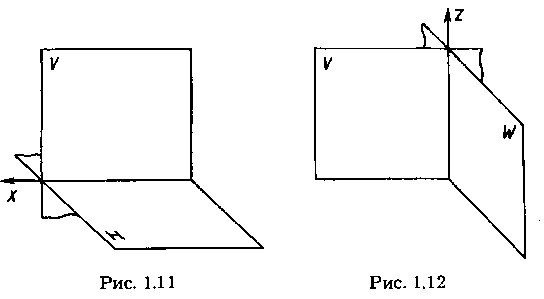
Для удобства проецирования в качестве двух плоскостей проекций выбирают две взаимно перпендикулярные плоскости (рис. 1.11). Одну из них принято располагать горизонтально — ее называют горизонтальной плоскостью проекций, другую — вертикально. Вертикальную плоскость называют фронтальной плоскостью проекций. Эти плоскости проекций пересекаются по линии, называемой осью проекций.

Ось проекций разделяет каждую из плоскостей проекций на две полуплоскости.

Обозначим плоскости проекций буквами: V — фронтальную, Н — горизонтальную, ось проекций — буквой х или в виде

дроби V/H. Плоскости V и Н образуют систему V, Н. (Наряду с указанными обозначениями плоскостей проекций в литературе применяют и другие обозначения, например буквой π с индексами.)

Плоскости проекций, пересекаясь, образуют четыре двугранных угла, из которых приведенный на рисунке 1.11 (с обозначениями граней V, Н) считают первым.

В промышленности чертежи многих деталей выполняют также в системе двух взаимно перпендикулярных плоскостей, пересекающихся по вертикальной оси проекций z (рис. 1.12). При этом фронтальной плоскостью проекций оставляют также плоскость V, а перпендикулярную к ней и обозначаемую W называют профильной плоскостью проекций.

В системе двух взаимно перпендикулярных плоскостей проекций горизонтальной проекцией точки называют прямоугольную проекцию точки на горизонтальной плоскости проекций;

фронтальной проекцией точки называют прямоугольную проекцию точки на фронтальной плоскости проекций.

Наглядное изображение построения проекций произвольной точки А в системе V, Н показано на рисунке 1.13. Горизонтальную проекцию, обозначенную а, находят как пересечение перпендикуляра, проведенного из точки А к плоскости Н, с этой плоскостью. Фронтальную проекцию, обозначенную а', находят как пересечение перпендикуляра, проведенного из точки А к плоскости V, с этой плоскостью.

Проецирующие прямые Аа' и Аа, перпендикулярные к плоскостям V и Н, принадлежат плоскости Q. Она перпендикулярна плоскостям проекций и пересекает ось проекций в точке а_х. Три взаимно перпендикулярные плоскости Q, V и Н пересекаются по взаимно перпендикулярным прямым, т. е. прямые а'а_х, аа_х и ось х взаимно перпендикулярны.

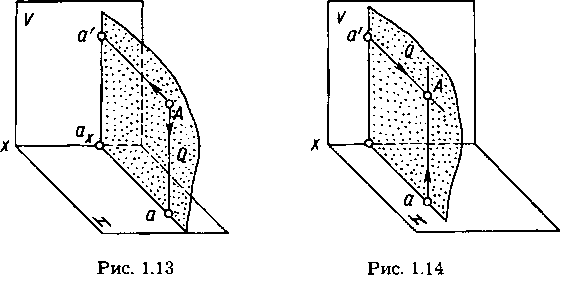
Построение некоторой точки А в пространстве по двум заданным ее проекциям — фронтальной а' и горизонтальной а — показано на рисунке 1.14. Точку А находят на пересечении перпендикуляров, проведенных из проекции а' к плоскости V и из проекции а к плоскости Н. Проведенные перпендикуляры принадлежат одной плоскости Q, перпендикулярной к плоскостям V и Н, и пересекаются в единственной искомой точке А пространства.

Таким образом, две прямоугольные проекции точки вполне определяют ее положение в пространстве относительно данной системы взаимно перпендикулярных плоскостей проекций.

В дальнейшем прямоугольные проекции точки в системе взаимно перпендикулярных плоскостей проекций будем называть ортогональными проекциями точки.

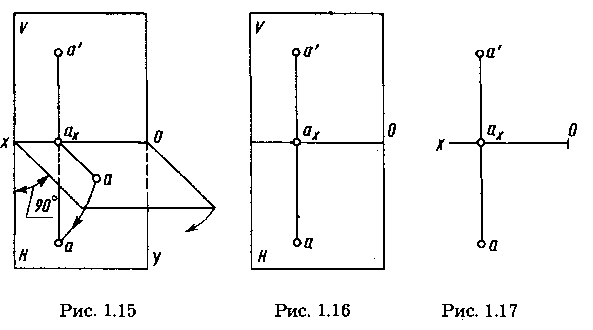
Рассмотренное наглядное изображение точки в системе V, Н неудобно ввиду своей сложности для целей черчения. Преобразуем его так, чтобы горизонтальная плоскость проекций совпадала с фронтальной плоскостью проекций, образуя одну плоскость чертежа. Это преобразование осуществляют (рис. 1.15) путем поворота вокруг оси х плоскости Н на угол 90° вниз. При этом отрезки а_х= а' и а_х = а образуют один отрезок а'а, перпендикулярный оси проекции, называемый линией связи. В результате указанного совмещения плоскостей V и Н получается чертеж — рисунок 1.16, известный под названием эпюр (от французского ериrе — чертеж, проект) или эпюр Монжа. Этот чертеж в системе V, Н (или в системе двух прямоугольных проекций) называют чертежом Монжа. Без обозначения плоскостей V и H этот чертеж приведен на рис. 1.17.