Пример определения высоты пирамиды и угла между ее гранями

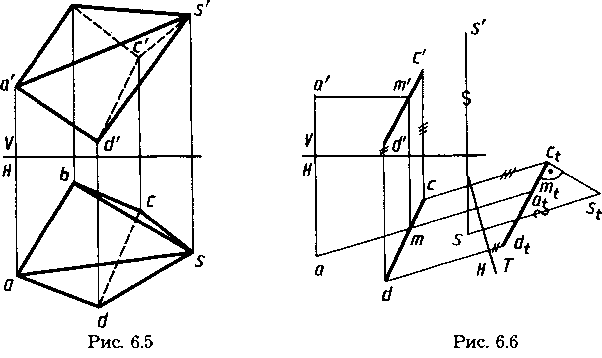
В представленной на рисунке 6.5 пирамиде, основание и грани которой являются плоскостями общего положения, требуется определить ее высоту (расстояние от вершины с проекциями s', s до основания с проекциями a'b'c'd', abcd) и двугранный угол между гранями с проекциями a'b's' , abs и a'd's', ads.

Указанные задачи можно решить способом перемены плоскостей проекций, рассмотренным в 5.2.

Определение расстояния от вершины до основания выполнено на рисунке 6.6. При этом плоскость основания ABCD задана проекциями а', а точки и d'c', dc отрезка. Новая плоскость проекций Т (Т перпендикулярна Н) выбрана перпендикулярной горизонтали с проекциями a'm, am основания (ось T/H перпендикулярна ат) и соответственно плоскости основания. На плоскость проекций Т часть основания пирамиды проецируется в отрезок dtct, расстояние от которого до проекции st, вершины и соответствует искомой высоте пирамиды.

Определение угла между гранями. Двугранный угол измеряют линейным углом, полученным в пересечении граней

двугранного угла плоскостью, перпендикулярной к обеим граням двугранного угла ф, а следовательно, и к линии их пересечения, т.е. к ребру двугранного угла. Определение угла ф между гранями пирамиды выполнено на рисунке 6.7, где двумя переменами плоскостей проекций ребро с проекциями a's', as двугранного угла, являющегося отрезком общего положения, переведено в проецирующее положение относительно плоскости проекций R.. Полученная на плоскости проекций R проекция drsr=arbr двугранного угла выражает его линейный угол.

При преобразовании система плоскостей проекций V, Н заменена вначале системой Н, Q (Q перпендикулярна Н),

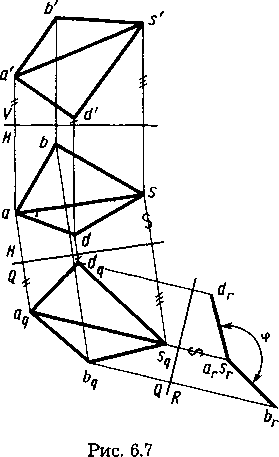
в которой плоскость Q выбрана параллельной ребру AS (ось H/Q || as). Затем система плоскостей проекций Н, Q заменена на систему Q, R (R перпендикулярна Q), в которой плоскость проекций R выбрана перпендикулярной ребру AS (ось Q/R перпендикулярна aqsq).