Применение вспомогательных сфер с переменным центром
Способ секущих сфер с переменным центром для построения линии пересечения двух поверхностей применяют при следующих условиях:
а) одна из пересекающихся поверхностей— поверхность вращения, другая поверхность имеет круговые сечения;
б) обе поверхности имеют общую плоскость симметрии (т. е. ось поверхности вращения и центры круговых сечений второй поверхности принадлежат одной плоскости — плоскости их симметрии);
в) плоскость симметрии параллельна плоскости проекций (это условие при необходимости может быть обеспечено преобразованием чертежа).
Рассмотрим некоторые примеры применения этого способа.
Построение линии пересечения прямого кругового конуса и наклонного кругового цилиндра (рис. 10.8), оси которых пересекаются. Пересекающиеся поверхности имеют общую плоскость симметрии, параллельную плоскости V и проходящую через их оси. Относительно этой плоскости симметрична и линия пересечения поверхностей. В дальнейшем изложении будут указываться построения проекций только видимых точек линии пересечения. Из характерных точек можно отметить четыре с проекциями а', е', к', п'. Они являются точками пересечения проекций очерковых линий.
Для построения проекций промежуточных точек, например b', находят центр и радиус вспомогательной сферы. Для этого на цилиндре проводят окружность, фронтальная проекция которой изображается отрезком 1'2'. Эту окружность можно рассматривать (рис. 10.8, а) как параллель множества сфер, центры
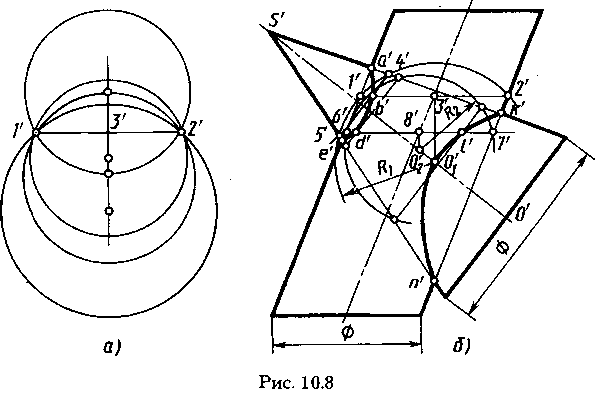
которых лежат на перпендикуляре—линии центров, проведенном из точки с проекцией 3' центра кругового сечения к плоскости окружности с проекцией 1'2'. Выберем (рис. 10.8, б) из сфер такую, центр которой с проекцией о1' находится в точке пересечения линии центров сфер и оси конуса SO (s'o'). Эта сфера радиусом R1=о1'1'=о1'2' пересекает конус по окружности, проецирующейся в отрезок 4'5'. Окружности с проекциями 1'2' и 4'5' лежат на поверхности одной вспомогательной сферы радиуса R1 и пересекаются между собой в двух точках, фронтальные проекции которых совпадают. На чертеже отмечена проекция b' видимой точки. Проекции последующих точек строят аналогично. Точка с проекцией d' построена с помощью вспомогательной сферы радиуса R2. Проекция о2' ее центра построена в пересечении проекции оси конуса с проекцией линии центров сфер к круговому сечению с проекцией 6'7' — перпендикуляром из проекции 8' к плоскости этого кругового сечения.
Отметим, что центр 02 второй сферы сместился относительно центра O1 первой сферы. Каждому круговому сечению наклонного цилиндра, используемому для построения линии пересечения, соответствует свой центр на оси конуса. Это и является основанием для названия способа — способ сфер с переменным центром.
Сфера радиуса R2 использована и для построения точки с проекцией l'.
Горизонтальные проекции точек линии пересечения строят или с помощью одноименных образующих цилиндра, или на одноименных проекциях его круговых сечений.
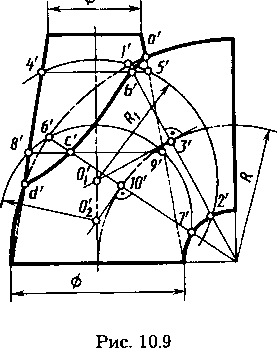
Построение линии пересечения прямого кругового конуса и тора, оси которых скрещиваются (рис. 10.9). Ось конуса параллельна плоскости V, ось тора перпендикулярна плоскости V, окружность центров осевых круговых сечений тора и ось конуса лежат в одной плоскости, параллельной плоскости V.
Две очевидные характерные точки: высшая с проекцией а' и низшая d' — являются точками
пересечения проекций очерков тора и конуса. Для построения проекций промежуточных точек, например проекции b', выполняют следующие построения. Выбирают на поверхности тора окружность, например с проекцией 1'2' с центром в точке с проекцией 3'. Перпендикуляр к плоскости этой окружности из точки с проекцией 3' является линией центров множества сфер, которые пересекают тор по окружности с проекцией 1'2'. Из множества этих сфер выбирают сферу с центром на оси конуса. Его проекция о1'. Эта сфера радиусом R1 пересекает конус по окружности с проекцией 4'5'. Пересечение проекций 1'2' и 4'5' является проекцией пары общих точек тора и конуса, т.е. линии их пересечения. На чертеже обозначена проекция b' одной из указанных точек— точки на видимом участке линии пересечения.
Построение проекций второй пары точек линии пересечения, из которых обозначена проекция с', выполнено с помощью отрезка 6'7' — проекции окружности на поверхности тора. Вспомогательная сфера для построения проекции с' — сфера радиуса R2 с центром, проекция которого о'2. Конус эта сфера пересекает по окружности с проекцией 8'9'. В пересечении проекций 6'7' и 8'9' окружностей находим проекцию с' искомой точки и симметричной ей на невидимой части пересекающихся поверхностей.
