Построение проекций цилиндрической винтовой линии

Цилиндрическая винтовая линия может рассматриваться как траектория движения точки, равномерно вращающейся

вокруг оси и одновременно перемещающейся в направлении этой оси. В виде цилиндрической винтовой линии остается след острия резца на поверхности равномерно вращающегося цилиндрического стержня при одновременном поступательном движении резца вдоль оси

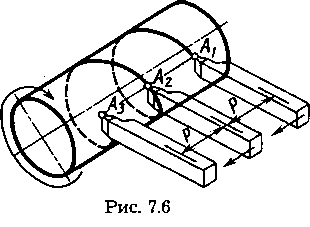
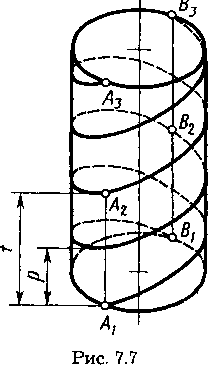
цилиндра. За один оборот цилиндра образуется один виток или оборот винтовой линии. Винтовая линия с двумя витками A1A2A3, оставленная концом резца на цилиндрической заготовке, показана на рисунке 7.6. Расстояние р, проходимое точкой вдоль оси за один оборот, называют шагом винтовой линии, расстояние от точки до оси вращения — радиусом винтовой линии. На одной поверхности цилиндра может быть несколько винтовых линий с одинаковым шагом, например две линии А1А2А3 и В1В2В3 на рисунке 7.7. Каждую линию в таком случае называют заходом, а шагом считают расстояние вдоль оси между соседними линиями. Число заходов обозначают п. Перемещение точки вдоль оси за один полный оборот в этом случае называют ходом t винтовой линии. С числом заходов п и шагом р ход t связан выражением: t = пр.

Построение на чертеже цилиндрической винтовой линии показано на рисунке 7.8. Для ее построения шаг (фронтальную проекцию o'o'i отрезков оси) и длину окружности цилиндра (горизонтальную проекцию окружности основания диаметром D) разбивают на равное количество частей п, обычно п=12, и нумеруют соответствующие образующие. Точка А винтовой линии при повороте на угол 2π/п перемещается вдоль оси на величину р/п или при п = 12 на 30° и р/12 соответственно, занимая последовательно положения с проекциями a₁', a₁, a₂', a₂, ..., a₁₂', a₁₂, a₁₃', a₁₃ за один оборот. Соединив последовательные положения этой точки на фронтальной проекции плавной линией, получают фронтальную проекцию винтовой линии, являющуюся синусоидой. На рисунке 7.8 поверхность цилиндра принята непрозрачной, поэтому верхняя половина витка показана как невидимая.

Различают правую и левую винтовые линии. Если точка движется по винтовой линии на фронтальной проекции слева-вверх-направо, то такую линию называют правой (см. рис. 7.8). Если движение справа-вверх-налево, то винтовая линия левая.

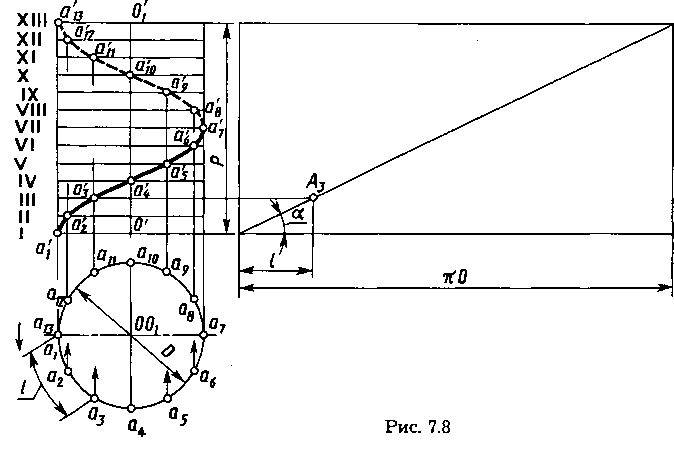
Развертка винтовой линии — прямая линия — показана на рисунке 7.8 справа. Угол подъема винтовой линии а. Значение его определяется по формуле:

tg a =p/πD.

Угол а характеризует крутизну подъема винтовой линии.