Пересечение прямой линии с проецирующей плоскостью

При построении точки пересечения прямой с проецирующей плоскостью исходят из рассмотренного выше положения о том, что плоскость, перпендикулярная плоскости проекций, проецируется на нее в виде прямой линии (см. 3.2). Следовательно, на этой прямой находится и соответствующая проекция точки пересечения заданной прямой с проецирующей плоскостью.

На рисунке 4.1, б горизонтально-проецирующая плоскость Q задана следами Q_v и Q_h (наглядное изображение — на рис. 4.1, а), прямая АВ — общего положения. Точка из пересечения одновременно принадлежит прямой АВ и плоскости Q. Следовательно, ее горизонтальная проекция к принадлежит одновременно горизонтальному следу Q_h и горизонтальной проекции прямой, т. е. является точкой их пересечения. По горизонтальной проекции к точки К на фронтальной проекции a'b' прямой находим фронтальную проекцию к' точки пересе-

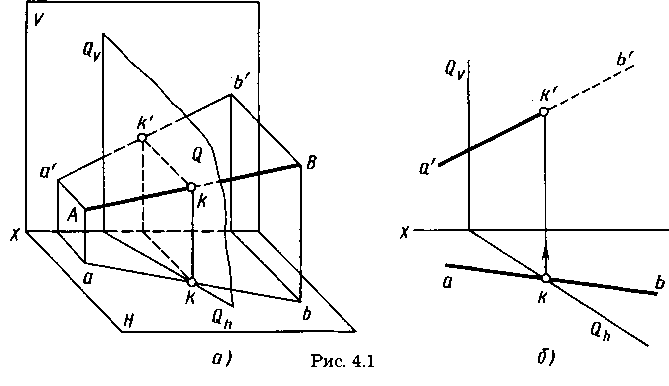
чения. Из горизонтальной проекции видно, что правее проекции к проекция kb находится между осью х и следом Q_h, т. е. плоскость Q находится перед прямой АВ и закрывает ее на фронтальной проекции. Условно считают плоскость непрозрачной, поэтому на чертеже фронтальная проекция к'b' показана для наглядности как невидимая штриховой линией. На сложных чертежах штриховые линии не применяют.

Некоторые условности изображения невидимых точек, линий, плоскостей. Условно считают, что данная плоскость непрозрачна. Поэтому точки, линии, участки другой плоскости, расположенные между плоскостью проекций и данной плоскостью, невидимы для наблюдателя, между которым и плоскостью проекций находятся изображаемые объекты. Если линии, точки, участки другой плоскости находятся между данной плоскостью и наблюдателем, то они видимы и закрывают точки, линии, участки данной плоскости, лежащие на одних проецирующих прямых.

Видимые отрезки линий изображают сплошными линиями, невидимые — штриховыми.

Анализ видимости линий обычно проводят путем анализа видимости точек, как это сделано при анализе видимости конкурирующих точек на скрещивающихся прямых (см. 2.4, рис. 2.22, 2.23).

Пример построения точки пересечения прямой общего положения с проекциями e'f, ef с горизонтально-проецирующей плоскостью в виде треугольника с проекциями а'b'с', abc показан на рисунке 4.2.

Фронтальная проекция т' точки пересечения М построена по ее горизонтальной проекции т, которая является точкой пересечения горизонтальных проекций ef прямой и acb треугольника. Аналогично отмечена видимость: левее от точки М плоскость треугольника AьC при взгляде спереди закрывает отрезок прямой, т. е. на фронтальной проекции левее точки т' прямая невидима до границы проекции а'с' плоскости треугольника.

Построение на чертеже точки пересечения фронтально-проецирующей плоскости, заданной следами Р_и, P_h и прямой с проекциями a'b', ab, показано на рисунке 4.3.

Фронтальная проекция к’ точки пересечения является точкой пересечения фронтального следа P_v и фронтальной проекции a'b' прямой. Горизонтальную проекцию к находят на горизонтальной проекции ab прямой на линии связи. Справа

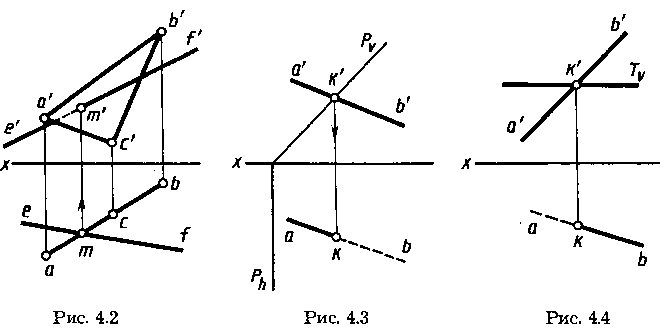
от точки К прямая АВ (луч КВ) закрывается сверху плоскостью Р, поэтому на горизонтальной проекции справа от точки К проекция kb прямой показана невидимой.

Аналогичное построение приведено на рисунке 4.4 для точки пересечения прямой АВ с горизонтальной плоскостью T(T_V). Фронтальная проекция к' точки пересечения является точкой пересечения следа T_v и проекции а'b'. Горизонтальная проекция к построена на горизонтальной проекции ab с помощью линии связи. На фронтальной проекции видно, что слева от точки к' проекция к'b' находится под проекцией T_v,, т. е. слева от точки К прямая АВ (луч КА) находится под плоскостью Т. На горизонтальной проекции слева от точки К проекция ка прямой показана невидимой.