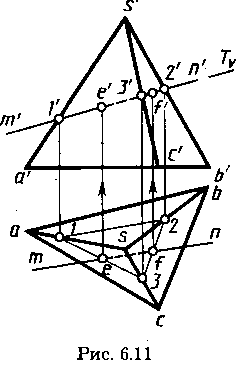
Пересечение многогранников плоскостью
При пересечении призмы или пирамиды плоскостью в сечении получается плоская фигура, ограниченная линиями пересечения секущей плоскости с гранями призмы или пирамиды.
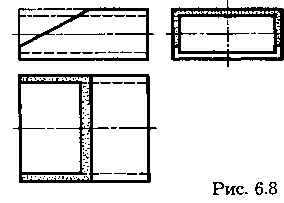
Простейший пример конструирования детали пересечением исходной заготовки в виде прямоугольной трубы плоскостью приведен на рисунке 6.8. В этом случае деталь — волновод изготавливают, отрезая часть заготовки по плоскости R (R,). Другой пример конструирования устойчивой подставки в виде усеченной пирамиды показан на рисунке 6.9. Наклонная площадка ABCD образована срезом верхней части пирамиды фронтально-проецирующей плоскостью S (Sv). Фронтальные проекции d, b', с', d' точек находятся на фронтальном следе Sv плоскости, а фронтальная проекция площадки ABCD совпадает со следом Sv. Профильная a"b"c"d" и горизонтальная abed проекции площадки построены по проекциям указанных точек на проекциях соответствующих ребер.
Построение натуральной величины сечения пирамиды плоскостью.
Во многих случаях требуется построить натуральный или истинный вид сечения тела плоскостью. На рисунке 6.9 для этой цели вверху слева применен способ перемены плоскостей проекций. В качестве дополнительной плоскости принята плоскость Т, параллельная плоскости S и перпендикулярная плоскости V Натуральный вид площадки — фигуры сечения atbtctdt. Другой вариант построения натурального вида наклонной площадки ABCD показан на рисунке 6.9 справа внизу — А0,В0,С0,D0. Для построения использованы новые координатные оси х1 и у1, лежащие в плоскости S. Ось х1 параллельна плоскости V, ось у1 перпендикулярна плоскости V
Координаты на оси х1 точек А0,В0,С0,D0 равны координатам по оси x1 фронтальных проекций а', b', с' d' этих точек. Координаты x1 точек с0 , с' по оси х1, равны нулю. Координаты У в, yD по оси у1 точек В0,, D0 равны координатам по этой оси (параллельной оси у) горизонтальных проекций b, d. Координаты по оси у1 точек А, С равны нулю. По указанным координатам на осях x1, у1 строят натуральную величину А0,В0,С0,D0 наклонной площадки ABCD.
Пирамида с вырезом. Как пример построения сечений несколькими плоскостями рассмотрим (рис. 6.10) построение пирамиды с вырезом, который образован тремя плоскостями — горизонтальной Т(Tv), фронтально-проецирующей R (Rv) и профильной Q (Qv). Горизонтальная плоскость Т (Tv) пересекает боковую поверхность пирамиды по пятиугольнику с горизонтальной проекцией k—l—g—f—4—k, стороны которого параллельны проекциям сторон основания пирамиды. Фронтально-проецирующая плоскость R (R,v) в пределах выреза пересекает боковую поверхность пирамиды по ломаной линии с горизонтальной проекцией 3—8—9—10—2 и с профильной проекцией 3"8"9"10"2". Профильная плоскость Q (Qv) пересекает в пределах выреза боковую поверхность пирамиды по ломаной с го-
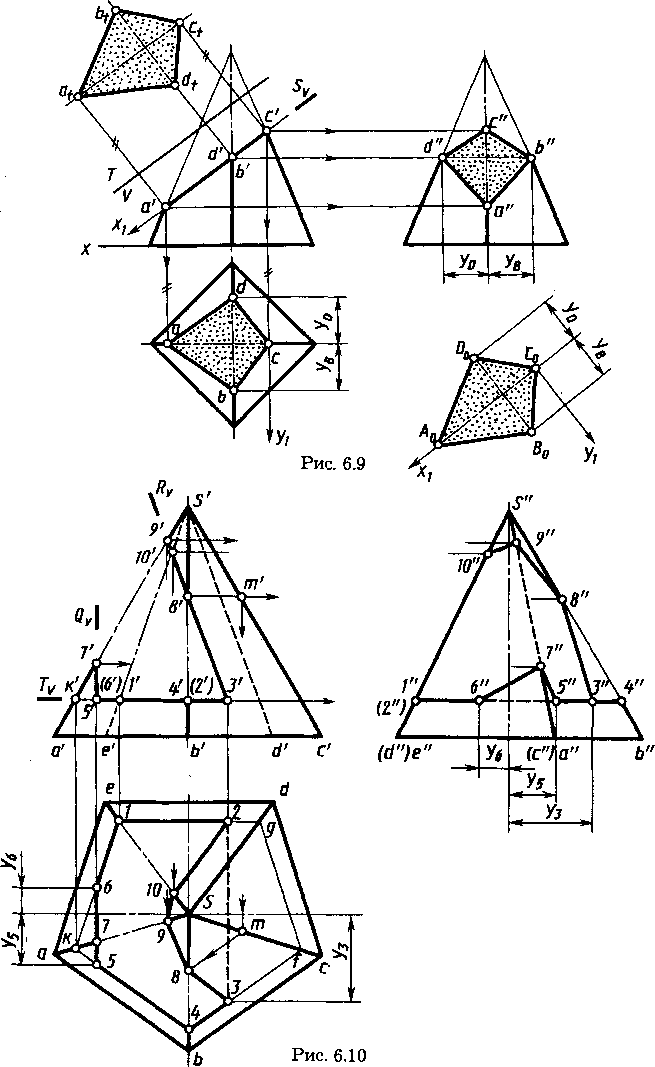
ризонтальнои проекцией в виде отрезка прямой 5— 7—б и с профильной проекцией 5"7"6".
Полученные точки соединяют в такой последовательности, чтобы две точки принадлежали одной секущей плоскости и одной грани пирамиды.