Параллельные проекции и их основные свойства

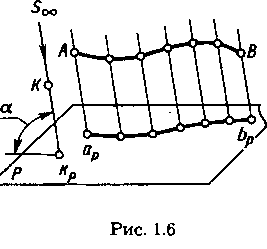
Параллельное проецирование (рис. 1.6) можно рассматривать как частный случай центрального проецирования, при котором центр проекций удален в бесконечность (5оо). При параллельном проецировании применяют параллельные проецирующие прямые, проведенные в заданном направлении относительно плоскости проекций. Если направление проецирования перпендикулярно плоскости проекций, то проекции называют прямоугольными или ортогональными, в остальных случаях— косоугольными (на рис. 1.6 направление проецирования указано стрелкой под углом а не равном 90° к плоскости проекций Р).

При параллельном проецировании сохраняются все свойства центрального проецирования, а также возникают следующие новые свойства.

1. Параллельные проекции взаимно параллельных прямых параллельны, а отношение длин отрезков таких прямых равно отношению длин их проекций.

Если прямые MN и KL (рис. 1.7) параллельны, то проецирующие плоскости Q и Т параллельны, так как пересекающиеся прямые в этих плоскостях взаимно параллельны: MN || KL по условию, Аа_р || Ссp || S. Следовательно, проекции т_рп_р и k_pl_p параллельны как линии пересечения параллельных плоскостей Q и T с плоскостью Р.

Отметим на прямой MN произвольный отрезок АВ и на прямой KL — произвольный отрезок CD. Проведем в плоскости Q через точку А прямую А—1 || арbр и в плоскости Т через точку С — прямую

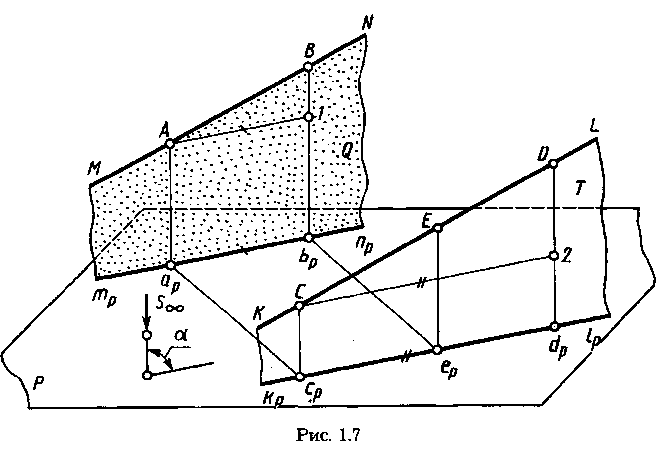
C—2 || cpd_p. Отрезки [A—1] = [apb_p], [C—2] = [Cpdp] как отрезки параллельных между параллельными. Отрезки С—2 || с,d_Р  || aрb_р и, следовательно, С— 2 || А— 1. Отрезки В— 1 || D—2 || S,  треугольник АВ—1 ~ треугольнику CD—2, так как все их стороны взаимно параллельны. Из подобия треугольников АВ— 1 и CD—2 следует:

|АВ|:|CD| = |А—1| : |С—2|= |арbp| : |c_pd_p|

Из рассмотренного следует:

а)    если длина отрезка прямой делится точкой в каком-либо отношении, то и длина проекции отрезка делится проекцией этой точки в том же отношении (рис. 1.8):

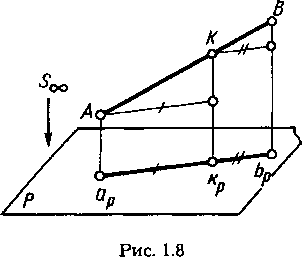
|АК|:|КВ| = |аркр|:|крbр|,

б)    проекции равных по длине отрезков взаимно параллельных прямых взаимно параллельны и равны по длине.

Это очевидно, так как (см. рис. 1.7) при |AB|:|CD|=1 будет |арbр| = | c_pd_p|. Поэтому при косоугольном проецировании в общем случае параллелограмм, ромб, прямоугольник, квадрат проецируются в параллелограмм.

2.    Плоская фигура, параллельная плоскости проекций, проецируется при параллельном проецировании на эту плоскость в такую же фигуру.

3.    Параллельный перенос фигуры в пространстве или плоскости проекций не изменяет вида и размеров проекции фигуры.

Параллельные проекции, как и центральные при одном центре проекций, также не обеспечивают обратимости чертежа. Применяя приемы параллельного проецирования точки и линии, можно строить параллельные проекции поверхности и тела. Параллельные проекции применяют для построения наглядных изображений различных технических устройств и их деталей, например аксонометрических проекций, рассматриваемых ниже.