Определение натуральной величины отрезка прямой общего положения и углов его наклона к плоскостям проекций

На рисунке 2.8 видно, что натуральная величина отрезка ВС прямой общего положения является гипотенузой прямоугольного треугольника ВС—1. В этом треугольнике один катет В—1 параллелен плоскости Н и равен по длине горизонтальной проекции отрезка ВС, а величина второго катета равна разности расстояний точек С и В до плоскости проекций Н ( |С—1| = Zc—zb=Δz).

Построения на чертеже для определения натуральной величины отрезка ВС прямой общего положения приведены на рисунке 2.9. В качестве одного катета принята горизонтальная проекция bс, длина другого катета |сС|=|с'l'|=Δz. Длина гипотенузы bс равна длине отрезка ВС.

Другое построение выполнено на фронтальной проекции. Проекция b’с’ отрезка взята за один катет прямоугольного треугольника. Длина другого катета равна разности расстояний от концов отрезка до плоскости V. Длина гипотенузы Вс' равна длине отрезка ВС.

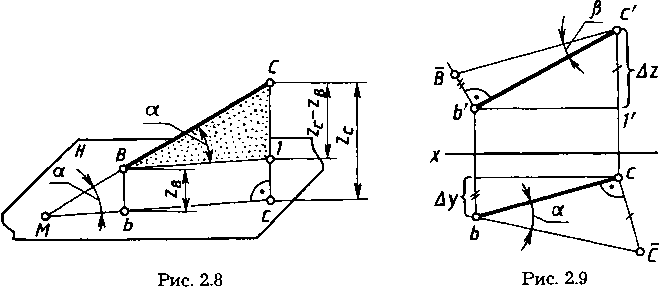
Итак, натуральную величину отрезка определяют как гипотенузу прямоугольного треугольника, одним из катетов которого является горизонтальная (фронтальная) проекция отрезка, другим — разность координат концов отрезка до горизонтальной (фронтальной) плоскости проекций. Этот метод иногда называют способом прямоугольного треугольника.

Угол между прямой и плоскостью проекций определяется как угол между прямой и ее проекцией на эту плоскость. На рисунке 2.8. таким углом между прямой ВС и плоскостью H является угол a (угол BMb). Угол а равен углу СВ—1, так как одна сторона МС общая, а две другие В—1 и МС параллельны.

Величину угла а определяют из того же треугольника СВ—1, что и натуральную величину отрезка ВС. На рисунке 2.9 показано, что угол a равен углу cBc. Угол β наклона прямой к фронтальной плоскости проекций определяется из треугольника b'с'В, построенного на фронтальной проекции отрезка: угол β равен углу b'c'B.