Общие сведения о поверхностях и их изображении на чертежах

В начертательной геометрии поверхность рассматривают как множество последовательных положений движущейся линии или другой поверхности в пространстве. Линию, перемещающуюся в пространстве и образующую поверхность, называют образующей. Образующие могут быть прямыми и кривыми. Образующие поверхность кривые могут быть постоянными и переменными, например закономерно изменяющимися.

Одна и та же поверхность в ряде случаев может рассматриваться как образованная движениями различных образующих. Например, круговой цилиндр может быть образован: во-первых, вращением прямой относительно неподвижной оси, параллельной образующей; во-вторых, движением окружности, центр которой перемещается по прямой, перпендикулярной плоскости окружности; в-третьих, прямолинейным движением сферы.

При изображении поверхности на чертеже показывают лишь некоторые из множества положений образующей. На рисунке 8.1 показана поверхность с образующей АВ. При своем движении образующая остается параллельной выбранному направлению MN и одновременно пересекает некоторую кривую линию CDE. Таким образом движение образующей АВ направляется в пространстве линией CDE.

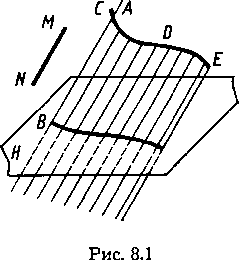
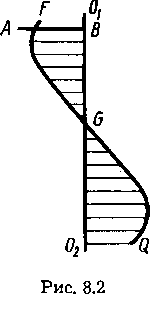
Линию или линии, пересечение с которыми является обязательным условием движения образующей при образовании поверхности, называют направляющей или направляющими. На рисунке 8.2 показана проекция поверхности, образованной движением прямой АВ по двум направляющим —

прямой 0102 (АВ перпендикулярно 0102) и пространственной кривой FGQ, не пересекающей прямую 0102.

Иногда в качестве направляющей используют линию, по которой движется некоторая характерная для образующей точка, но не лежащая на ней, например центр окружности.

Из различных форм образующих, направляющих, а также закономерностей образования конкретной поверхности выбирают те, которые являются наиболее простыми и удобными для изображения на чертеже поверхности и решения задач, связанных с нею.

Иногда для задания поверхности используют понятие определитель поверхности, под которым подразумевают совокупность независимых условий, однозначно задающих поверхность. В числе условий, входящих в состав определителя, различают геометрическую часть (точки, линии, поверхности) и закон (алгоритм) образования поверхности геометрической частью определителя.

Рассмотрим краткую классификацию кривых поверхностей, принятую в начертательной геометрии.

Линейчатые развертываемые поверхности. Поверхность, которая может быть образована движением прямой линии, называют линейчатой поверхностью. Если линейчатая поверхность может быть развернута так, что всеми своими точками она совместится с плоскостью без каких-либо повреждений поверхности (разрывов или складок), то ее называют развертываемой. К развертываемым поверхностям относятся только такие линейчатые поверхности, у которых смежные прямолинейные образующие параллельны, или пересекаются между собой, или являются касательными к некоторой заданной пространственной кривой. Все остальные линейчатые и все нелинейчатые поверхности относятся к неразвертываемым поверхностям.

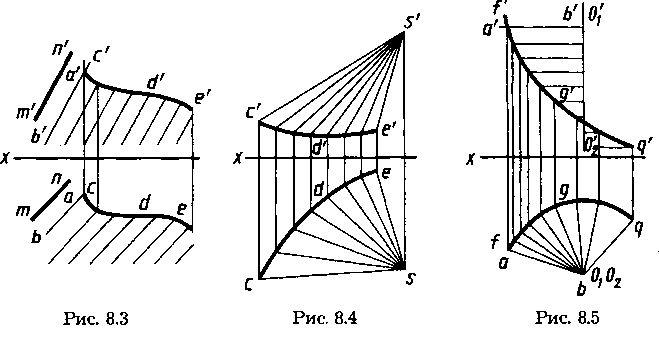
Развертываемые поверхности — цилиндрические, конические, с ребром возврата или торсовые. У цилиндрической поверхности образующие всегда параллельны, направляющая — одна кривая линия. Изображение на чертеже ранее показанной в пространстве цилиндрической поверхности (см. рис. 8.1) представлено на рисунке 8.3. Частные случаи — прямой круговой цилиндр, наклонный круговой цилиндр (см. рис. 9.17, направляющая —

окружность, плоскость которой расположена под углом к оси цилиндра и с центром на его оси). У конических поверхностей все прямолинейные образующие имеют общую неподвижную точку — вершину, направляющая — одна любая кривая линия. Пример изображения конической поверхности на чертеже — рисунок 8.4, проекции вершины s', s, направляющей c'd'e', cde. Частные случаи — прямой круговой конус, наклонный круговой конус (см. рис. 10.10, справа). У поверхностей с ребром возврата или торсовых прямолинейные образующие касательны к одной криволинейной направляющей.

Линейчатые неразвертываемые поверхности: цилиндроид, коноид, гиперболический параболоид (косая плоскость). Поверхность, называемая цилиндроидом, образуется при перемещении прямой линии, во всех своих положениях сохраняющей параллельность некоторой заданной плоскости («плоскости параллелизма») и пересекающей две кривые линии (две направляющие). Поверхность, называемая коноидом, образуется при перемещении прямой линии, во всех своих положениях сохраняющей параллельность некоторой плоскости («плоскости параллелизма») и пересекающей две направляющие, одна из которых кривая, а другая прямая линия (рис. 8.5, см. также рис. 8.2). Плоскостью параллелизма на рисунке 8.5 является плоскость Н, направляющие — кривая с проекциями a'g'q', agq, прямая с проекциями o₁'o₂', o1o.  В частном случае, если криволинейная направляющая — цилиндрическая винтовая линия с осью, совпадающей с прямолинейной направляющей, образуемая поверхность — винтовой коноид, рассматриваемый ниже.

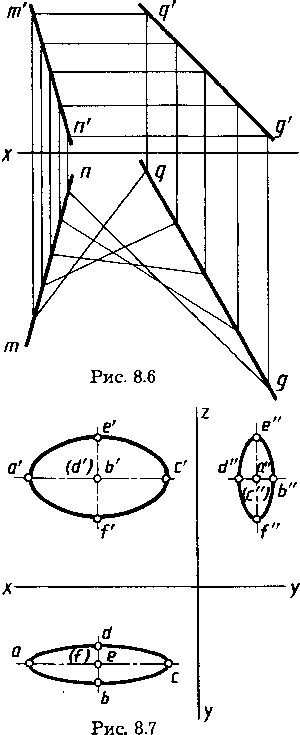
Чертеж гиперболического параболоида, называемого косой плоскостью, приведен на рисунке 8.6. Образование этой поверхности можно рассматривать как результат перемещения прямолинейной образующей по двум направляющим — скрещивающимся прямым параллельно некоторой плоскости параллелизма. На рисунке 8.6 плоскость параллелизма — плоскость проекций Н, направляющие — прямые с проекциями т'п',  тп и q'g',  qg.

Нелинейчатые поверхности. Их подразделяют на поверхности с постоянной образующей и поверхности с переменной образующей.

Поверхности с постоянной образующей в свою очередь подразделяют на поверхности вращения с криволинейной образующей, например сфера, тор, эллипсоид вращения и др. (см. рис. 8.16, 8.13), и на циклические поверхности, например поверхности изогнутых труб постоянного сечения, пружин.

Поверхности с переменной образующей подразделяют на поверхности циклические с переменной образующей, топографические поверхности аффинных и подобных линий и т. д. Чертеж поверхности второго порядка — эллипсоида — приведен на рисунке 8.7. Образующая эллипсоида — деформирующийся эллипс, одна из проекций которого, например, d"e"b"f". Две направляющие — два пересекающихся эллипса, плоскости которых ортогональны и одна ось общая, например с проекциями a'e'c'f' и adcb. Образующая пересекает направляющие в крайних точках своих осей. Плоскость образующего эллипса при перемещении остается параллельной плоскости, образованной двумя пересекающимися осями направляющих эллипсов. Циклические поверхности с переменной образующей имеют образующую — окружность переменного радиуса, направляющую — кривую, по которой перемещается центр образующей, плоскость образующей перпендикулярна к направляющей.

Каркасную поверхность задают некоторым множеством линий или точек поверхности. Обычно такие линии — плоские кривые, плоскости которых параллельны между собой. Два пересекающихся семейства линий каркаса образуют сетчатый каркас поверхности. Точки пересечения линий образуют точечный каркас поверхности. Точечный каркас поверхности может быть задан и координатами точек поверхности. Каркасные поверхности широко используют при конструировании корпусов судов, самолетов, автомобилей, баллонов электронно-лучевых трубок (см. форзац).

Из указанных поверхностей рассмотрим более подробно винтовую.