Общие сведения о пересечении поверхностей

Общие сведения. Форма большинства сложных и ответственных деталей приборов и машин образована комбинацией различных элементарных тел, расположенных в пространстве так, что поверхности их пересекаются между собой. Поэтому важным этапом конструирования таких деталей является определение границ исходных поверхностей, которыми и являются линии их взаимного пересечения.

Выше уже рассмотрено построение линий пересечения некоторых поверхностей и тел между собой: двух плоскостей (4.2, 4.4), многогранников (6.6).

В данной главе рассмотрены общий прием построения линии пересечения двух криволинейных поверхностей между собой, а также некоторые частные случаи пересечения при различном взаимном расположении поверхностей и их положении относительно плоскостей проекций.

Общий способ построения линии пересечения двух поверхностей между собой. В общем случае линию пересечения двух поверхностей между собой строят по точкам, которые находят с помощью вспомогательных секущих поверхностей (или плоскостей).

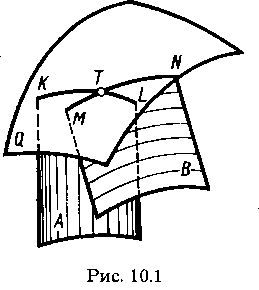
Две криволинейные поверхности А и В (рис. 10.1) пересекаются третьей секущей вспомогательной поверхностью Q. Находят линии пересечения KL и MN вспомогательной поверхности с каждой из заданных. Точка Т пересечения построенных линий KL и MN принадлежит линии пересечения заданных поверхностей А и В.

Повторяя такие построения многократно с помощью аналогичных вспомогательных поверхностей, находят необходимое число общих точек двух поверхностей для проведения линии их пересечения.

Сформулируем общее правило построения линии пересечения поверхностей:

выбирают вид вспомогательных поверхностей; строят линии пересечения вспомогательных поверхностей с заданными поверхностями;

находят точки пересечения построенных линий и соединяют их между собой плавной кривой.

В качестве вспомогательных поверхностей выбирают такие, линии пересечения которых с заданными поверхностями проецируются на чертеж в графически простые линии — прямые, окружности. В качестве вспомогательных поверхностей можно, например, использовать плоскости или сферы. Рассмотрим их применение.

Заметим, что если одна из исходных поверхностей линейчатая, то задача построения линии пересечения в этом случае может быть сведена к построению точки пересечения прямой (образующей линейчатой поверхности) со второй заданной поверхностью (см. 9.5). При построениях применяют способы преобразования чертежа, если это упрощает и уточняет построения.

При построении точек линии пересечения поверхностей вначале находят те точки, которые называют характерными или опорными.