Некоторые особые случаи пересечения поверхностей
В некоторых случаях расположение, форма или соотношения размеров криволинейных поверхностей таковы, что для изображения линии их пересечения никаких сложных построений не требуется. К ним относятся пересечения цилиндров с параллельными образующими, конусов с общей вершиной, соосных поверхностей вращения, поверхностей вращения, описанных вокруг одной сферы.
Изображения пересечения цилиндров с параллельными образующими приведены на рисунке 10.10 слева, конусов с общей вершиной — справа.
Соосные поверхности вращения. Изображения пересечений соосно расположенных различных поверхностей вращения приведены на рис. 10.11. Конус, пересекающийся с двумя цилиндрами разного диаметра (рис. 10.11, а), часто используют при конструировании как переход от одного диаметра к другому.
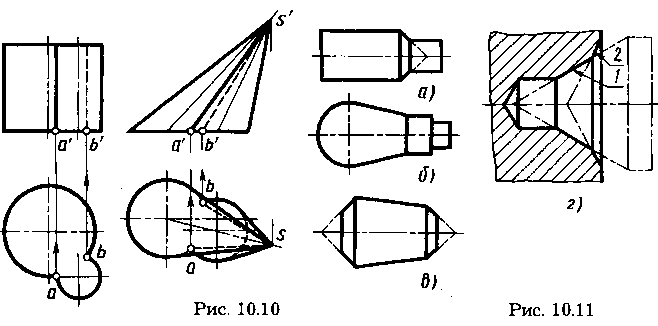
Конус, сопряженный со сферой, с переходом на цилиндры (рис. 10.11, б), широко используют в качестве деталей механизмов управления — рукояток.
Комбинацию из трех соосных пересекающихся конусов (рис. 10.11, в) применяют при конструировании деталей, называемых штифтами или роликами. Крайние конические поверхности, называемые фасками, служат для упрочения кромки детали и предохранения тем самым от забоин основной рабочей конической поверхности. Комбинация из пересекающихся трех соосных конусов образует центровое гнездо для обработки деталей в центрах. Для предохранения от повреждений рабочей конической поверхности 1 при соприкосновении (ударах) с другими деталями служит наружный конус 2.
Пересечение поверхностей, описанных вокруг одной сферы (рис. 10.12). В этом случае линиями пересечения поверхнос-
тей 2-го порядка являются две плоские кривые 2-го порядка, изображаемые на плоскости, параллельной осям поверхностей, в виде прямолинейных отрезков. Выше уже были приведены некоторые примеры таких пересечений.
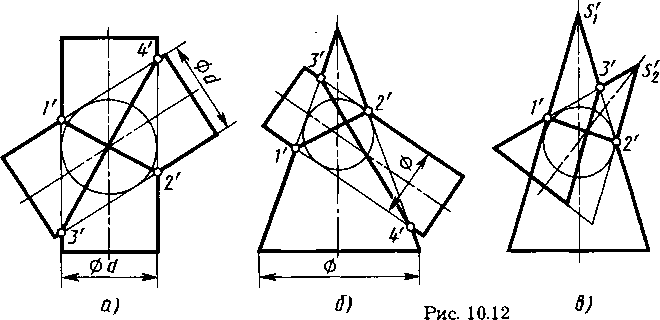
Другие примеры изображения линии пересечения поверхностей вращения, описанных вокруг одной сферы, рассмотрены на рисунке 10.12.
В случаях, показанных на рис. 10.12 а, б, поверхности двух цилиндров, конуса и цилиндра пересекаются по двум эллипсам с проекциями 1'2' и 3'4'.
В случае, показанном на рис. 10.12, в, пересечения конусов с вершинами S1 и S2, у которых имеются две параллельные образующие, линии пересечения — эллипс с проекцией 1'2' и парабола с вершиной в точке с проекцией 3'.
Рассмотренные примеры пересечения двух поверхностей вращения, описанных вокруг одной сферы, являются частными случаями, следующими из теоремы Монжа: две поверхности 2-го порядка, описанные около третьей поверхности 2-го порядка (или в нее вписанные), пересекаются между собой по двум кривым 2-го порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания.
Пересечение поверхностей, когда одна из них проецирующая (рис. 10.13). Если одна из пересекающихся поверхностей проецирующая, то задача построения линии пересечения двух поверхностей упрощается и сводится к построению недостающих проекций кривой линии на одной из поверхностей по одной заданной проекции линии (см. 8.3). На рисунке 10.13 горизонтальная проекция линии пересечения прямого кругового цилиндра и сферы совпадает с горизонтальной проекцией цилиндра. Фронтальная и профильная проекции линии построены по их принадлежности сфере с помощью проекций вспомогательных линий на сфере. Отметим характерные (опорные) точки линии пересечения, пользуясь горизонтальной проекцией. Высшая и низшая точки (их проекции 2', 2, 2" и 1', 1, 1") лежат в плоскости симметрии фигуры, проходящей через центр сферы с проекциями о', о и ось цилиндра с проекциями о1'о1', o1. Горизонтальная проекция плоскости симметрии — прямая, проходящая через проекции о и o1. В пересечении этой прямой с проекцией цилиндра отмечаем горизонтальные проекции 2 и 1 высшей и низшей точек линии пересечения. Заметим, что точка 2 — ближайшая
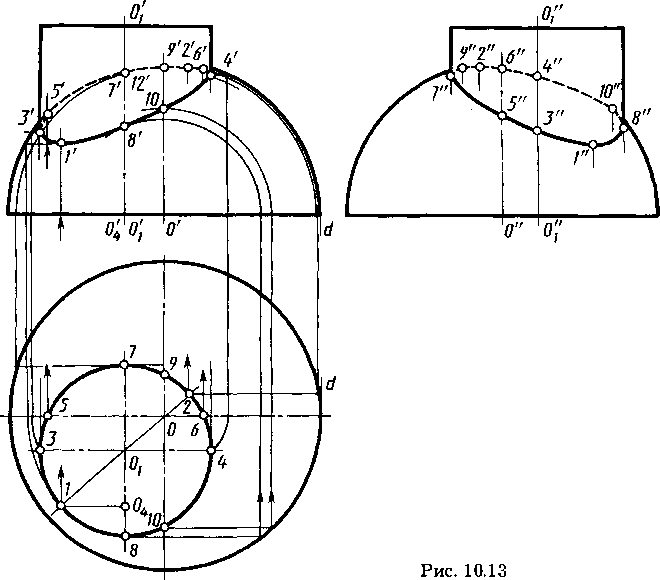
к высшей точке сферы, а точка 1 — наиболее удаленная от нее. Точки 3 и 4 — крайние левая и правая на фронтальной и горизонтальной проекциях, их профильные проекции 3", 4" на проекциях образующих, совпадающих с проекцией оси цилиндра. Точки 5 и 6 находятся на главном меридиане сферы, их фронтальные проекции 5' и 6' — на фронтальном очерке сферы, профильные 5" и 6" — на профильной проекции вертикальной оси сферы. Точки 7 и 8 — ближайшая к плоскости V и наиболее удаленная от нее, их фронтальные проекции 7' и 8' — на проекции оси цилиндра, а профильные 7" и 8" — на крайних левой и правой проекциях образующих. Точки 9 и 10 имеют проекции 9' и 10' на фронтальной проекции вертикальной оси сферы, проекции 9" и 10" — на профильной проекции очерка сферы.
Рассмотренные особенности характерных точек позволяют легко проверить правильность построения линии пересечения поверхностей, если она построена по произвольно выбранным
точкам. В данном случае десяти точек достаточно для проведения плавных проекций линии пересечения. При необходимости может быть построено любое количество промежуточных точек.
Проекция 1' низшей точки построена с помощью проекций параллели сферы. Проекция 2' высшей точки построена с помощью проекций окружности радиуса o'd' на поверхности сферы, плоскость которой параллельна плоскости V. Аналогичные построения остальных проекций точек линии пересечения ясны из чертежа.
Построенные точки соединяют плавной линией с учетом особенностей их положения и видимости.
