Винтовые поверхности
Винтовые поверхности весьма широко используют в технике для формообразования деталей различного назначения.
Винтовая поверхность образуется при движении прямолинейной образующей по двум направляющим, одна из которых винтовая линия, другая — ось винтовой линии, которую образующая пересекает под постоянным углом.
Прямая винтовая поверхность. У прямой винтовой поверхности угол между образующей и осью равен 90°. Это винтовой коноид или прямой геликоид. Чертеж прямой винтовой поверхности приведен на рисунке 8.8. Перемещаясь в направлении, как указано стрелкой на горизонтальной проекции, отрезок АВ движется вдоль оси вверх и образует правую винтовую поверхность. Проекции а'5b'5, а'6 b'6,, а'7 b'7, а'8 b'8, а'9 b'9 условно показаны двумя линиями (они «удаляются» от наблюдателя).
В сечении прямой винтовой поверхности (рис. 8.9) плоскостями, перпендикулярными оси или проходящими через ось, получаются отрезки прямолинейной образующей. Используя их, можно построить точки на винтовой поверхности. Так, на рисунке 8.9 по горизонтальной проекции а точки А построена ее фронтальная проекция a' на фронтальной проекции образующей 1'2' в секущей плоскости Q (Qh). По фронтальной проекции
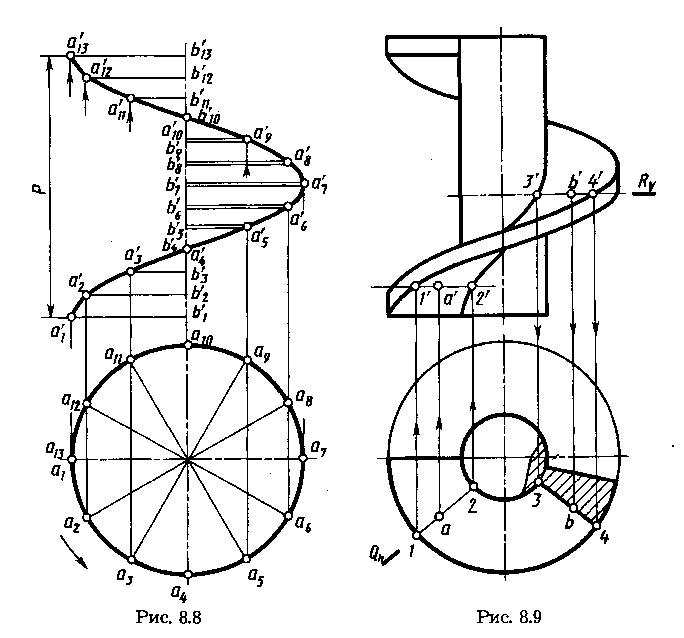
b' точки В построена ее горизонтальная проекция b на горизонтальной проекции образующей 3—4 в секущей плоскости R (Rv).
Косая винтовая поверхность. Если у винтовой поверхности угол между образующей и осью не равен 90°, то ее называют косой винтовой поверхностью. Изображение косой винтовой поверхности — наклонного геликоида приведено на рисунке 8.10, а. Проекции отрезка АО — образующей изображены в ряде последовательных положений: от первого до тринадцатого. Точка А образующей перемещается по винтовой линии. Соответствующие положения проекций точки О отмечают на оси, руководствуясь тем, что проекция отрезка АО на ось вращения постоянна по величине (l).
Построение сечения косой винтовой поверхности плоскостью, перпендикулярной оси, показано на рисунке 8.10, б. Такая плоскость пересекает поверхность по кривой линии — спирали Архимеда. Построение сечения выполняют по линиям каркаса — точкам С1, С2, С3, С4, С5 пересечения секущей плоскости Т (Tv) с образующей винтовой поверхности в ряде последовательных положений 1—О11, 2— O21, 3—О31, 4—О41, 5—О51, а также с винтовой линией в точке Сo (со', с0).
Для построения горизонтальных проекций с1, с2, с3, с4, с5 точек спирали Архимеда проводят горизонтальные проекции образующей винтовой поверхности в ряде произвольных положений: о — 1, о—2, о—З, о — а4,, о—5. В проекционной связи на фронтальной проекции винтовой линии отмечают фронтальные проекции 1', 2', 3', а4', 5' точек. Через них, учитывая, что величина проекции образующей на ось винтовой поверхности постоянна (ее значение 1 отмечено на чертеже для построения точки о1'), строят фронтальные проекции
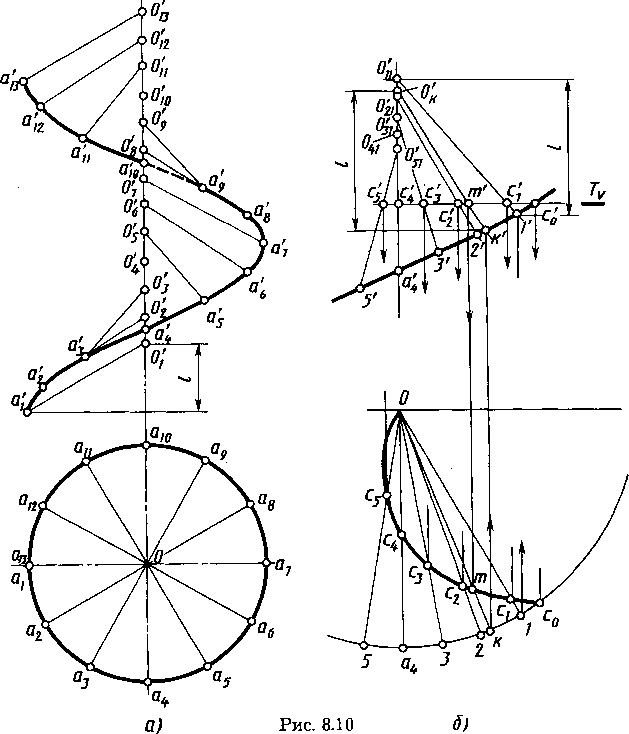
образующих о'111', о'212', о'313', о'а4', o'515'. В пересечении этих фронтальных проекций с фронтальным следом Tv секущей плоскости отмечают фронтальные проекции с с1', с2', с3', с4', c5' и по ним в проекционной связи строят горизонтальные проекции с1, c2, c3, c4, c5 искомых точек на соответствующих горизонтальных проекциях образующей. Через построенные точки проводят плавную кривую.
Если задана фронтальная проекция произвольной точки М винтовой поверхности, то ее горизонтальную проекцию строят с помощью сечения плоскостью, перпендикулярной оси, как это рассмотрено на рисунке 8.10, б. Если задана горизонтальная проекция точки (m), то через нее проводят горизонтальную проекцию ок образующей, строят фронтальную проекцию о'кк' по проекции к' и величине l — проекции образующей на ось винтовой поверхности. На построенной проекции о'кк' образующей отмечают фронтальную проекцию т' точки М.
