Использование в технике винтовых поверхностей (подсказано природой) — одно из замечательных достижений пытливой человеческой мысли в области техники.
В основе образования резьбы лежит винтовое движение некоторой фигуры, слагающееся из равномерных поступательного и вращательного движений относительно прямой, называемой осью винтового движения (осью винта).
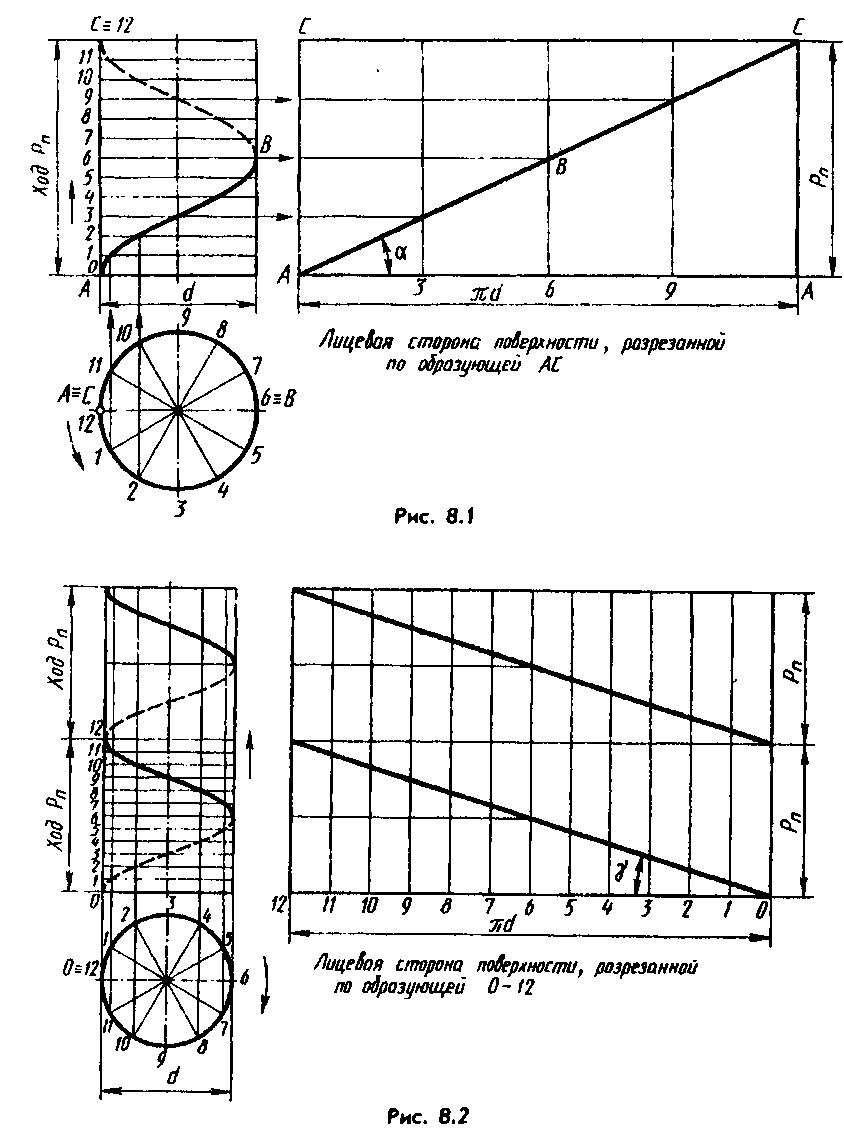
Винтовое движение может быть правым и левым. Если движение совершает точка, то производимую ею пространственную кривую называют винтовой линией (гелисой), правой (рис. 8.1) или левой (рис. 8.2).
Цилиндрическая винтовая линия образуется равномерным движением точки вдоль прямой (образующей цилиндра вращения), равномерно вращающейся (без скольжения) вокруг данной прямой, ей параллельной (оси цилиндра).
Участок винтовой линии, пройденный точкой за один ее оборот вокруг оси, называют витком гелисы (участок ABC на рис. 8.1), а расстояние между начальной и конечной точками витка (точки Л и С), измеренное по линии, параллельной оси резьбы, — ходом Рн винтовой линии.
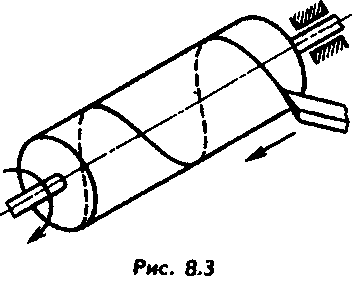
Если острие резца подвести к поверхности цилиндра, вращающегося с постоянной скоростью, а резец перемещать вдоль оси цилиндра также с постоянной скоростью, то острие резца опишет на поверхности цилиндра винтовую линию (рис. 8.3).
На рис. 8.1 показано построение правой цилиндрической винтовой линии. Ход и окружность основания цилиндра делят на одинаковое число равных частей, например на 12, горизонтали и точки нумеруют в направлениях, указанных стрелками. Затем из точки 1 проводят линию связи до пересечения с горизонталью 1, из точки 2— до пересечения с горизонталью 2 и т. д.
Через полученные точки проводят плавную кривую. Из построения видно, что фронтальная проекция гелисы является синусоидой.
Если принять цилиндрическую поверхность непрозрачной, то видимая часть АВ половины витка будет иметь подъем вправо. На развертке цилиндра винтовая линия преобразуется в прямую — гипотенузу АС. Следовательно, цилиндрическая гелиса — геодезическая линия, кратчайшим образом соединяющая в общем случае на поверхности цилиндра вращения две любые ее точки
Угол а — угол подъема винтовой линии. Касательная к гелисе в любой ее точке образует с осью постоянный угол а. При своем скольжении вдоль гелисы касательная прочертит на пл. П1 эвольвенту окружности
Аналогично строят проекции левой цилиндрической винтовой линии и ее развертку. На рис. 8.2 показано построение двух ее витков. Видимые части витков здесь имеют подъем влево.
Коническая винтовая линия образуется равномерным движением точки вдоль прямой (образующей конической поверхности), равномерно вращающейся вокруг пересекающейся с ней другой прямой — оси конуса. Ее построение (на рис. 8.4 показано построение двух витков правой гелисы) аналогично построению цилиндрической гелисы, с тем лишь отличием, что на то же число равных делений, на которое разделен ход, делят радиус окружности основания конуса. Деления нумеруют в на-правлениях, указанных стрелками. Затем из точки 1 проводят линию связи до пересечения с горизонталью 1, из точки 2 — до пересечения с горизонталью 2 и т. д. Через полученные точки проводят плавные кривые.
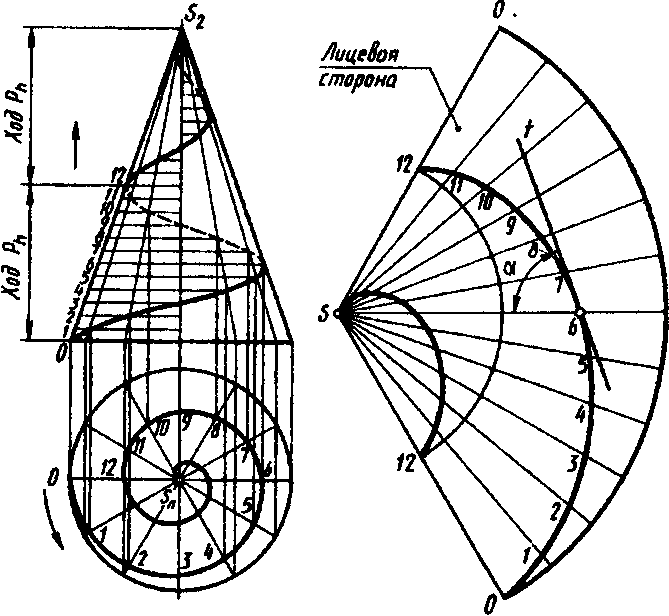
Фронтальная проекция гелисы — синусоида с уменьшающейся высотой витков («Затухающая кривая»), горизонтальная — спираль Архимеда. Винтовая линия на конусе не является геодезической, как это видно из развертки поверхности конуса, на которой гелисы преобразовались в спирали Архимеда, пересекающие образующие конуса под постоянным углом а.
Винтовые линии могут быть построены на любой поверхности вращения, в частности в технике они используются на сфере (рис. 8.5) и гиперболоиде вращения.
Винтовые поверхности образуются при винтовом движении произвольной линии (в частном случае, поверхности, например сферы).
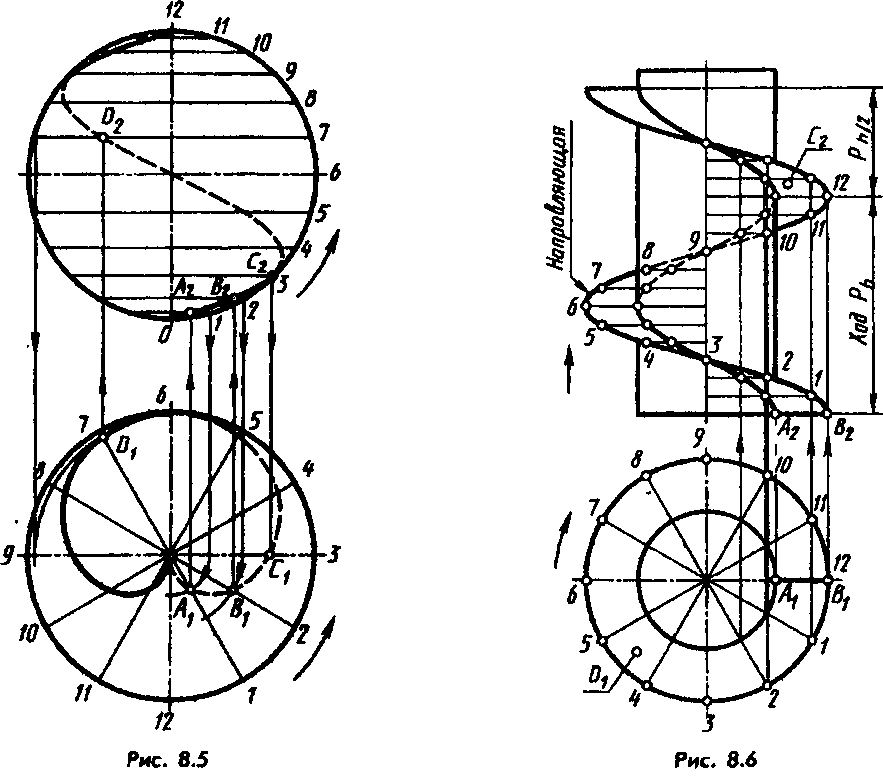
Наибольшее применение в технике имеют линейчатые винтовые поверхности (геликоиды), образованные движением отрезка прямой.
На рис. 8.6 показано построение поверхности левого прямого геликоида, ограниченной двумя винтовыми линиями. Производящий отрезок АВ скользит по направляющей гелисе, пересекая во всех своих положениях ее ось под углом 90° (или иначе, сохраняя параллельность горизонтальной плоскости проекций).
Ход и окружность (горизонтальную проекцию гелисы) делят на одинаковое число равных частей и из точек 1, 2, 3 и т. д. проводят линии связи до пересечения с одномерными горизонталями.
Видимость элементов поверхности, если считать цилиндр не-прозрачным, определяют, как и на рис. 8.1 и 8.2.
На рис. 8.7 производящий отрезок АВ скрещивается с осью направляющей гелисы a (a1, a2) под углом 90°, во всех своих положениях касаясь направляющего цилиндра и, следовательно, сохраняя параллельность горизонтальной плоскости проекций. Такую винтовую поверхность называют винтовым цилиндроидом. Очевидно, производящий отрезок при своем движении касается цилиндра по гелисе b (b1, b2).
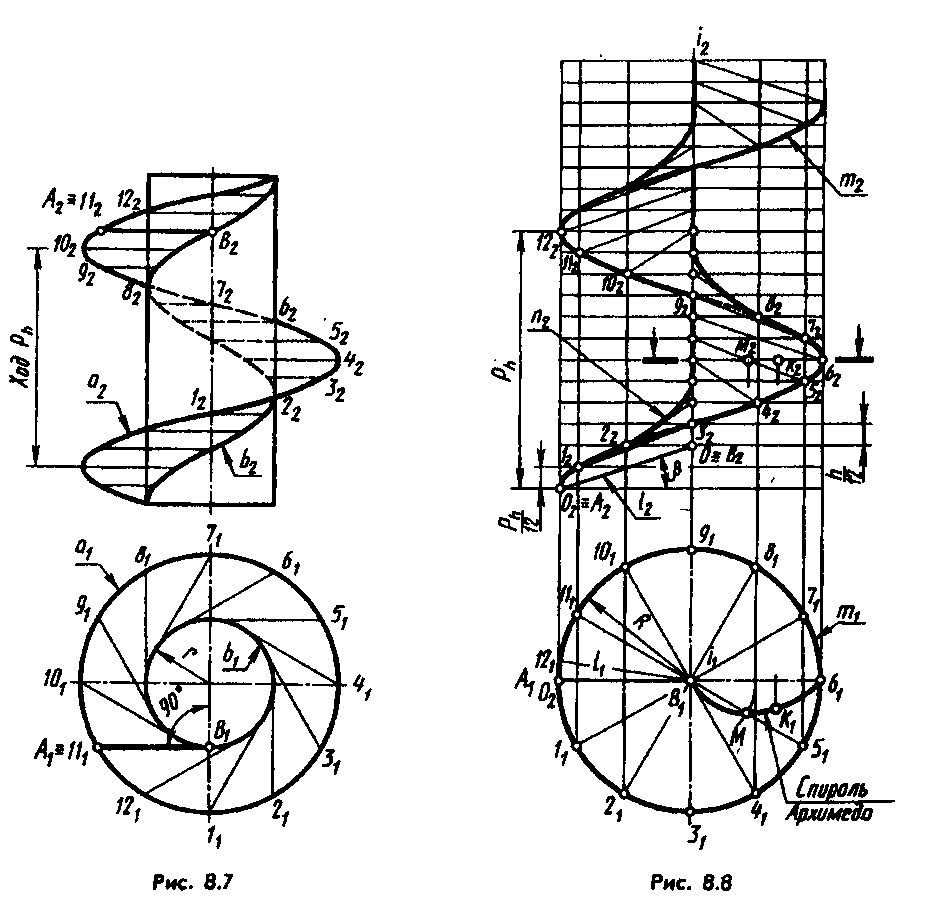
Производящий отрезок АВ, скользя по направляющей гелисе, может пересекать ее ось или скрещиваться с ней под некоторым постоянным острым углом.
В первом случае геликоид называют наклонным или архимедовым (нормальное сечение — спираль Архимеда, рис. 8.8), во втором — конволютным (рис. 8.9). Производящий отрезок касается некоторого цилиндра, радиус которого равен расстоянию между скрещивающимися прямыми.
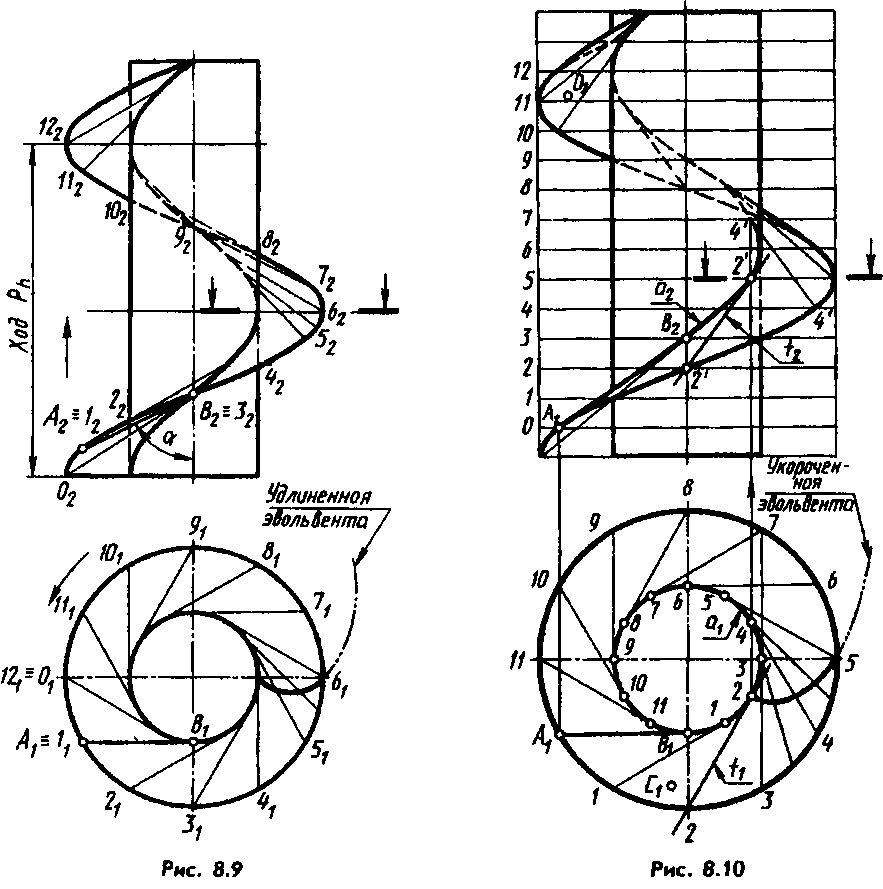
Геликоид может быть также образован движением прямой, сохраняющей касание к направляющей гелисе a (рис. 8.10). Такой геликоид называют развертывающимся или эволъвентным (его нормальное сечение — эвольвента окружности), или винтовым цилиндрическим торсом.
На рис. 8.11 показана винтовая цилиндрическая лента. Ее образование и построение не требуют пояснений.
На образующей цилиндра можно отметить любое число точек, перемещающихся вдоль нее с одинаковой скоростью: При вращении образующей все точки опишут гелисы одинакового хода. На рис. 8.12 показаны три гелисы, образованные точками Л, В, С, расположенными на равных расстояниях Р. Такие гелисы лежат в основе образования многозаходных резьб.
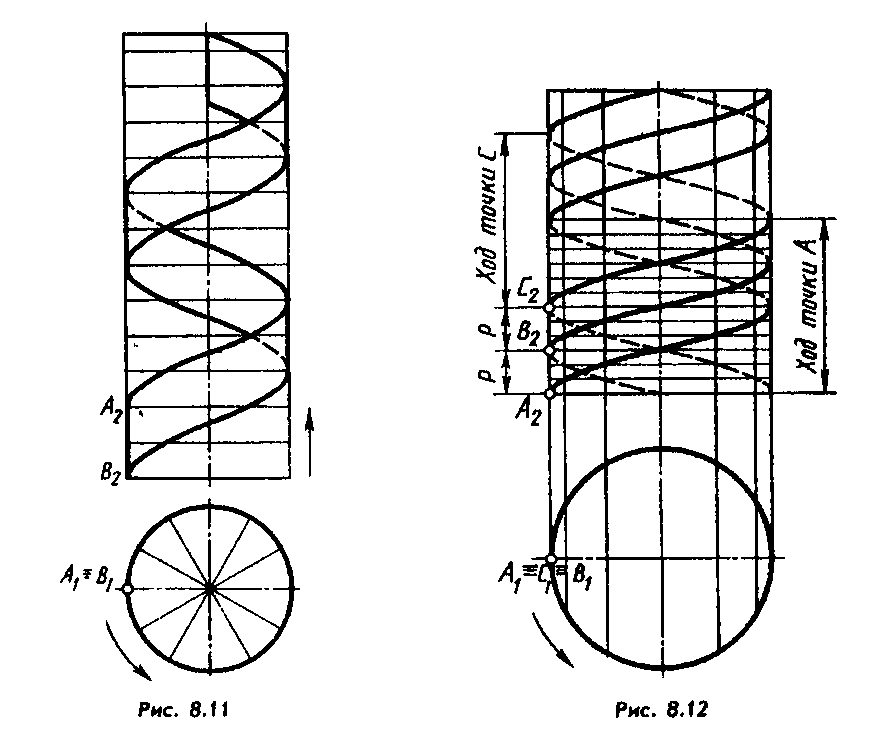
Резьба образуется при винтовом движении некоторой плоской фигуры, задающей так называемый профиль резьбы, расположенной в одной плоскости с осью поверхности вращения (осью резьбы).
В зависимости от формы профиля резьбу называют треугольной, квадратной, трапецеидальной, круглой.
Часть резьбы, образованной при одном повороте профиля вокруг оси, называют витком. При этом все точки производящего профиля перемещаются параллельно оси на одну и ту же величину, называемую ходом резьбы.
Различают правую и левую резьбы в зависимости от того, какая винтовая линия лежит в основе резьбы, правая или левая.
Если ось наружной резьбы расположить вертикально перед наблюдателем, то у правой резьбы видимая часть витков поднимается слева направо, у левой резьбы — справа налево (рис. 8.13).
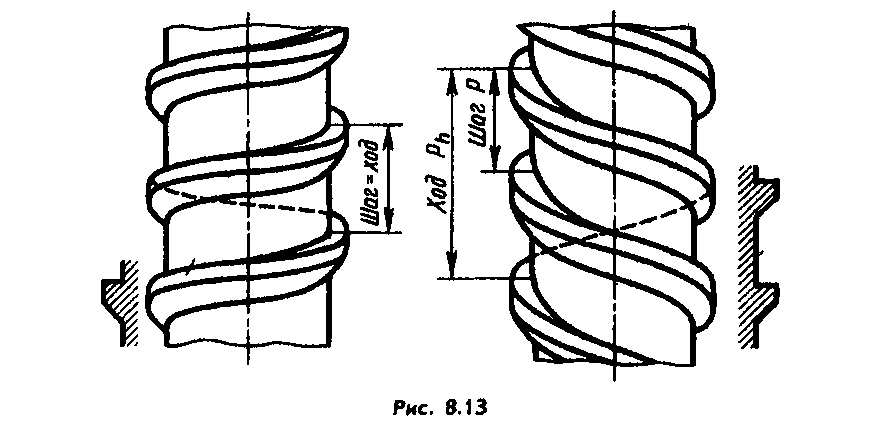
Если профиль перемещается по поверхности цилиндра вращения, резьбу называют цилиндрической (наиболее широко применяемой в технике), по поверхности конуса вращения — конической, по поверхности гиперболоида вращения — глобоидной.
Резьба может быть выполнена на стержне (наружная резьба) и в отверстии (внутренняя резьба).
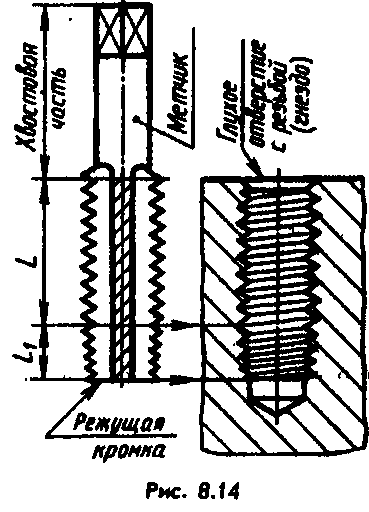
Резьбы, показанные на рис. 8.13 и 815, — наружные, на рис. 8.14 — внутренняя.
Резьбу, образованную движением одного профиля, называют одно-заходной, образованную движением двух, трех и более одинаковых про-филей, — многозаходной (двух-, трехзаходной и т. д.). В связи с этим введено понятие шаг резьбы, обозначаемый прописной латинской буквой Р — расстояние по линии, параллельной оси резьбы между средними точками ближайших одноименных боковых сторон профиля резьбы, лежащими в одной осевой плоскости по одну сторону от оси вращения — ГОСТ 11708—82 (СТ СЭВ 2631—80). Очевидно, ход Рh=nР, где п — число заходов (рис. 8.13). У однозаходных резьб ход равен шагу. Под шагом однозаходной резьбы подразумевают ход— расстояние, на которое переместится деталь с резьбой (винт при неподвижной гайке или гайка при неподвижном винте) за один оборот.